-
../../index.html: emC overview page
-
../../../emc/deploy/src_emC-2021-08-14-source.zip: Used sources
-
https://github.com/JzHartmut: Archive of emC
-
../../../smlk/index.html: Simulink stuff
-
../../../StimuliSel/html/StimuliSel.html: It is used here, see example
1. Approach
The PID controlling is familiar at all. It is known. PID means Proportional, Integral and Differential part of controlling in closed loop__. But sometimes different implementation approaches are necessary to discuss.
The here presented PID controller are Function Blocks in objectorientated C language or C++ implementation both for integer and float arithmetic proper for embedded controller, which runs in the same kind also in Simulink S-Functions. An adaption to other simulation tools such as Modelica is planned.
2. Math
The output of the controller depends on the controlling error (sometimes also named e)
which is wx = w - x where w is the reference value (sometimes also named r).
and x is the value to control, often the measured value or the output from the system or environment.
Shorten to the shortens: The w for the reference value instead r is familiar in the German and Europe,
it is the letter before x. w x y are the important letters for control.
The r is often used for other designations too. Hence w is more concise.
e for 'error' is also a too common shorten, hence wx is used here, it is more cocise.
The output is calulated in Math as:
y = kP * ( wx + ∫ 1/Tn * wx*dt + Td * dwx/dt )
dt is the differential of the time. On a discrete system it is the step time.
dwx is the change of wx in the dt time.
This is the simple theory. In practice there are some additional approaches:
-
1) The integral ∫ is undetermined. It means it can run away. Only in a closed loop the integral is guaranteed in a defined range, because in a closed loop the value of
wxdepends on the outputyitself. If the system has no other limitationswxis in middle= 0, so the integrator remains in the expected range. But if the system has limitations, it means that a valuexorwxcannot be delivered for the possibley, then the loop is not really closed. It is broken because of the limitation and the integrator goes away to unrealistic values. That should be prevented. This effect is named 'integration wind-up' -
2) All values come from a sampled system with a limited sampling rate.
-
3) For the differential the
dwxis the difference of the input from one step to the next. This difference can be less and hence inaccurate, only as mean value accurate. For that reason thedwxis usual built with an additional smoothing. -
4) Another effect for the D-part should be regarded: A measurement input
xhas usual a limited resolution. The input values are discontinuous in the value range. Building a difference with slowly changed physical input values results in suddenly step by one because of the resolution. Usual the resulting gain of the D-part delivers an output >1 for an input step =1. This results in a restless of the output. Of course because of the feedback of the system the values are in middle stable. The restless of the actuator signalydoes not force a restless in the system because this fast restless is filtered by the system (environment). But the actuator may be very volatile, which is not desired. The smoothing which is preferred for point 3) decreases this effect because the step of 1 of the input is divided in smaller steps. -
5) But: An additional smoothing in the D-part reduces the effect of the D-part. The smoothing time should be higher (at least 2 times) than the Td. Non smoothing of D is better for stability.
-
6) There are some discussions about "serial" and "parallel" form, whereas the shown serial from is more familiar in Europe. The "parallel" form is:
y = kP * wx + ∫ 1/Ti * wx * dt + Td * dwx/dt
The difference between the "parallel" and the "serial" form is only that the kP factor is used in the serial form for all parts. The here named Ti = Tn/kP, and the Td should be also divide. That is only a difference in offering the parameter, not in any principle. But the serial (European) form is more practical. Look on the Bode-plot for logarithm magnitude. Sorry, it is very schematic (TODO spend time for graph):
\
\ Tsd
\ /---
\ /
\ /
Tn\-------kP------/Td
-----++-------------++------0 dB----> fq
Ti Td
In the serial form, if kP is higher, the whole curve is shift vertical. All timings remain, which are related to system’s behavior time. It means if one tune the controller by adjusting kP, the relation between the times of the controller and the system times remain, only the feed forward gain is changed:
\ /---
\ / Tsd
\ /
Tn\-------kP------/Td
-----+--.---------.--+-------0 dB----> fq
Tn Td
For the parallel style the following occures on changing only kP:
\
\ Tsd
\ /---
Tn\---------kP--------/Tde
\ /
\ /
---+--+-------------+--+--------0 dB----> fq
Tn Ti Td Tde
Only the middle part which is related to kP, is moved up. The factors for Ti and Td remains, therefore, the oblique lines remain. But the kink frequency for Tn and the effective Td between the oblique lines of the I and D and the horizontal line for P are moved to left and right. Hence the kink frequency are no more related of that one of the system .
In conclusion the implementation of the PID control uses the serial form.
In the bode plots of magnitude the smoothing of the D part is also regarded, it is the Time Tsd.
3. Some implementation details
3.1. resolution of the integrator
The integrator part of PID may be slow, it should be adjust a less difference to get a zero value of the remaining controlling error
It is usual not sufficient to use a float type for the integrator. Why:
The float format has a mantissa of 24 bit, and hence a resolution of 2-23..2-24 or 0.00000006..0.00000012.
Your factor for the growth of the integral may be for example 0.0001 because the integration time is 10000 * Tstep,
it is 500 ms for 50 µs step time, an expectable value.
Then on a difference wx = 0.001, no more is added because the product is < 2-23.
0.001 is 0.1%, and this is the remaining error. The digital integration hangs.
An analog integrator is better.
But you see it depends on the timing relations. If you have only fast integration times,
or you use slow integration times with accepted error, then float may be sufficient.
For a specific solution you can decide whether a float resolution of the integrator is sufficient.
But for a common usage you have an additional necessary decision which complicates the development.
Hence a common way is: Using double. You have a resolution of 0.00000000000001, that’s enough.
A simple decision is: Using double instead float for all.
Why it is worse for most embedded controlling? :
Often embedded control processors have float arithmetic on hardware, not double.
Using double is a simple decision in C programming, but has impact to the calculation time.
The calculation time for double is maybe 10 times more then for float
because it is not simple "using two float operations for one double`".
`double is possible of course, but with specific machine instructions.
The worse decision is: general using double. If you have in the moment enough calculation time,
some enhancements may be destroy this approach.
The integrator of a PID control has usual the output range of the actuator. It is defined. It means, not float, instead fix point is proper for that. It is also not necessary to increase the accuracy or resolution for small values. Small values should be handled in the same resolution, the resolution of the actuator is given.
Hence, three solutions are possible:
-
1) Use a PID-controller as a whole in fix point arithmetic, because the actuator range is fix.
-
2) Use
int32only for the integrator. It increases the resolution from 0.00000006..0.00000012 to 0,000000002..0,000000005. 256 times more. -
3) Use
int64only for the integrator. The resolution is better thandouble.
The solution 1) is of course proper for a controller, which has no float arithmetic.
It is recommended to use either an int32 format for all, or int16 for input calculation
and int32 for the integrator, or int32 for input calculation and int64 for the integrator.
In opposite to float vs. double a 32 bit addition in a 16 bit controller
or a 64 bit addition in a 32 bit controller is only the double effort,
and it is only necessary for the integrator itself, not for all.
It is proper.
But, the solution 1) is not optimized for a controller, which supports float in its hardware.
Why? float is fast, if supported.
In opposite, integer arithmetic needs usual additional shift operations for multiplication.
It is real slower than float.
Hence the solution 2) or 3) is more proper for a float supporting controller.
In conclusion, several implementations of PID_ctrl_emC are offered in the emC library
and also as Simulink SFBlocks:
-
PIDi_Ctrl_emC: It works withintfor input values andint32as integrator. Becauseintdepends on the processor, it works withint16for cheap processors, whereint16is usual sufficient, and also fast. If you use a 32-bit-processor,intis usual a 32 bit width value and executable in one machine state, also fast. But the parameter calculation uses nevertheless sometimesfloat. It is more proper to calculate, and the calculation step time for parameters is usual slower, or only on initialization or on demand in the back loop. -
PIDf_Ctrl_emC: It works withfloatfor the input values and withint32for the integrator, proper for floating point processors. -
_step64_PIDf_Ctrl_emC: It works withfloatfor the input values and withint64for the integrator, proper for floating point processors, with higher resolution. The 64 bit variant uses the same data and the same parameterstruct. In thePIDf_Ctrl_emCdatastructthere is space for the 64-bit integrator, using a union. The not used 32 bit for 32 bit integration should not be a problem. Additional a compiler switch “DEF_PIDf32_Ctrl_emC” can be set on compilation for a specific 16- or 32-bit-target.
A special int16 PID or int32 PID is not offered. If you use a 16 bit processor,
often the lesser and native solution of 16 bit is proper. For a 32 bit processor,
calculation with int32 is not a higher effort and hence anyway possible.
3.2. Integral windup
If the input value wx as controlling error is given,
then the integrator of the PID ctrl growths, either to positive or negative.
On a closed loop in a near static state the input value is anyway zero or is oscillating near zero,
so the integrator does not go away. That is expected.
But, if any false condition is met, especially an opened loop in control, or an actuator limitation, and a controlling error remains, maybe also temporary for a little bit longer time, the integrator goes to its limits.
The worse scenario is, the integrator is not limited and the addition in machine code overflows. That is not usable.
Hence the so named 'integrator windup prevention' is very substantial.
There are more possible solutions. But usual the windup is only a secondary problem. It should be prevented, but in normal states it is not present. Hence a simple solution should be given.
The windup preventation for all emC PID control works in the following manner:
-
1) Generally the output of the controller can be limited to a changeable value. Because of the fix point property of the integrator the maximum possible value is given per initial parameterization. But a lower limit can be given too and can be changed any time.
-
2) This lower limit for the sum of P+I+D for the output of the controller can be depend on a necessary actuator limitation. If the actuator is limited, or should be limited, then the controller output can be limited to a proper value. For limitation you should / can use the operation
setLim_PID*_Ctrl_emC(…). The default value is the parameterized limit, if this operation is not called. -
3) If this limitation occurs, then the I part stops integration, it holds its value.
-
4) The integrator does not run to the limit also by itself. This behavior is proper because a limitation may occur because of a high disturbance, then the disturbance is gone, and the state after is sometimes the same. The integrator has approximately the same value, it is only a little bit changed on beginning of disturbance before limitation.
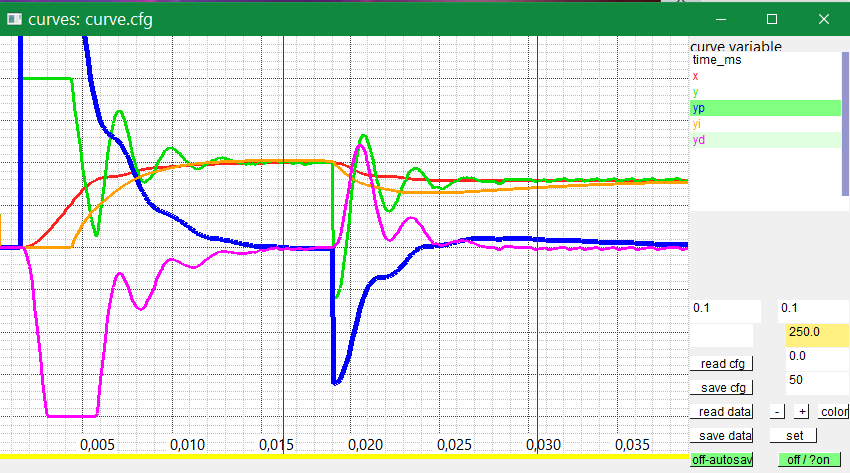
See the following result in closed loop as example:
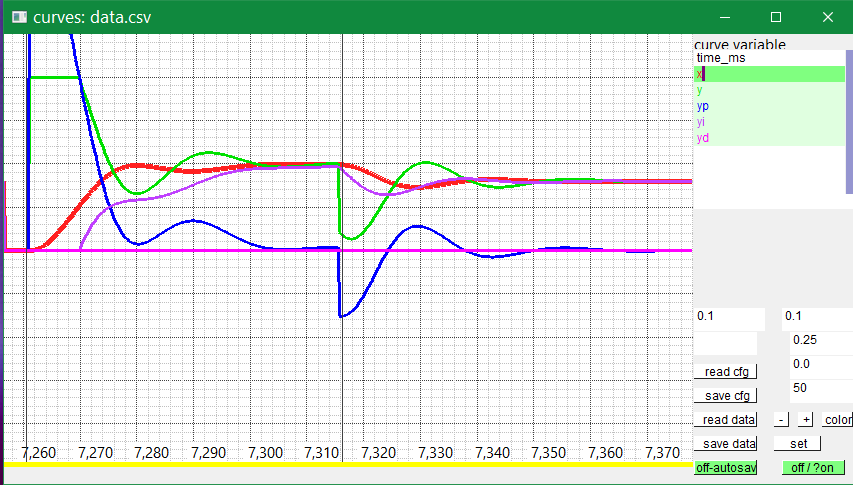
This example can be found in emC/test/cpp/emC_Test_Ctrl/test_PIDx_Ctrl.cpp. Parameters:
float kP = 4.0f, Tn = 0.004f, Tsd = 0.0005f, Td = 0; float fT1 = 0.01f, fT2 = 0.05f, fT3 = 0.1f;
The red curve is the x value, the output of the environment or system.
As you can see, the system is a little bit sluggish.
It needs a while till the output is changed though the output of the controller
is on max for the step response, the green curve.
It is a smoothing 3th order with the above shown factors (fT ~= Tstep/Ts).
If the integrator starts immediately, it will reach a too high value
during limitation, and on left limitation the integrator is too high.
The integrator curve (violet) is firstly hold on its current value (0 because it is a step response from 0). Why?
The correct feedback for the integrator is broken by the limitation. The integrator has an abbreviating behavior in comparison to the normal unlimited reaction, till the system is in a proper range. Hence it is helpful that the integrator does not work, holds its own value while limitation of the output. Only if the limitation is left, the proper calculated behavior for non limitation situation allows to calculate the integrator. Then, for this example, the integrator reaches a value near the necessary output in an expected time. Because of the system is 3th order, you see an oscillation for fast control.
In the diagram above you also see right side a lesser step response without limitation.
To see and compare the effect of this integrator wind-up prevention, compare to the following image, where this wind-up is switched of (by changing the PID software):
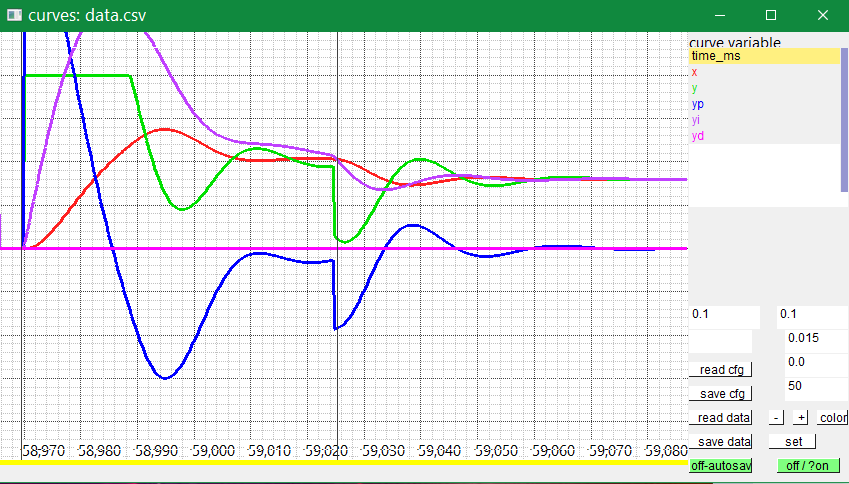
As you see, the integrator, violett curve, starts immediately and runs to an overflow. The output of the environment (red) overruns because of the longer time high output. It needs additional time to capture the correct value of controlling.
The question for the algorithm is: Need the integrator an extra limitation additional to the output limitation (software calculation time effort). The answer is no, because if the integrator is in the proper range, the addition of the P value is anytime in the same order as the direction of integrator changing. It means if the output is not limited, the integrator can work and will not reach the limit.
But: What’s happen if the limitation itself is changed to a value lesser than the current integrator value?
Then of course the integrator value should be checked whether it is range to the new limit.
That is implemented in the setLim_PIDx_Ctrl_emC(…) operation
and only executed if the limits are changed. This may be done in another step time
or only on demand, it does not use calculation time in the normal step routine.
The C-code for the PIDf with wind-up shows as:
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
y = wxP + dxP + thiz->yIntg + thiz->yAdd;
if(y >= thiz->limf) { // limitation necessary:
y = thiz->limf; // limit the output
if(thiz->qI.qI32 > 0x3F000000) {
thiz->qI.qI32 = 0x3F000000; // limit the integrator,
}
else if(thiz->qI.qI32 < -0x3f000000) {
thiz->qI.qI32 = -0x3f000000;
}
}
else if(y < -thiz->limf) { // same for negative limit
y = -thiz->limf;
}
else if(thiz->disableIntg ==0) { // integrate for next step only if not limited
int32 wxP32i = (int32)(f->fI * wxP); //growth for integrator
//Note: It is possible that a possible limitation was not detected just now,
//but it is effective in the next step time.
//Then the following is true:
//1) The max. value for qI32 in this moment is 0x3f00 correspond to fIy and fIx.
// An numeric overflow can never occur if Tn > 32 * Tstep (16 >= 0x7e00/0x01ff)
// That is a very less Tn, it is tested on parametrizing.
//2) An overdrive of the integrator for one step can occure
// because the integration is done after limit check.
// But this is only one time, only the integration of one Tstep.
// It is not effective for wind-up because it is integrated back
// in the next step time after left limitation.
ASSERT_TEST_emC(wxP32i <= 0x01ffffff && wxP32i >= -0x01ffffff, "overflow possible", wxP32i, thiz->qI.qI32 );
thiz->qI.qI32 += wxP32i; // use integer for exact integration.
thiz->yIntg = (int32)((thiz->qI.qI32)) * thiz->par->fIy; // float used.
}
else {
// // for test, manual changed yIntg is taken.
thiz->qI.qI32 = (int32)(thiz->par->fIx * thiz->yIntg); // Note: The I part is not limited
}
thiz->yctrl = y; // store output, after maybe limited
The wind-up preventing solution is very simple. It is combined with the limitation. It does not need additional calculation time.
You see that the integrator is calculated after building the y value.
That is admissible and more simple for the machine code.
But if you are very near on the limit, this addition can cause a value over the limit.
That is not a problem for the algorithm, because in the next step time
the limitation is detected and the integration is not done.
But you should not stay on the limits of the numeric value range.
Elsewhere an overflow may occur.
This overflow is safely prevented if it is checked in the parameter calculation
that the growth, calculated with the limited P-part, is not too high.
That is done. The assertions (ASSERT_emC(…)) are always true.
It is only for test and documentation.
3.3. How the D part works
The D part of a PID control should stabilize the control. If the D-part is correct tuned, then a fast change of the input signal decreases the output, so that it should be slower. That is the view in the timing. From view of stabilization criteria (https://en.wikipedia.org/wiki/Nyquist_stability_criterion) the D-part forces a phase advance, so the Nyquist-point is passed right side. So the theory.
The output decreasing effect of the D-part is sometimes misunderstood.
But look, the feedback value in the closed loop is used with - sign.
Fast changes of the feedback value from the environment or system (x)
forces a negative impact on the controller output.
Only if the D-part is too high, it oscillates.
But, from view of the reference value, the effect of the D-part is positive.
The controller input is usual (w-x) whereby w is the reference value
and x is the feedback from the outer system or environment.
It means that change of the reference value has a high increasing effect to the controller output.
Regarding the last statement,
it is interesting that sometimes the D-part should not be built with the control error
(w - x), instead only with the controlled value x.
Then the stabilization effect is also given, because the loop is closed.
But a change of the reference value w does not force a D-part as 'acceleration'.
Especially on a step response the D-Part will be high on beginning
because of the suddenly high change of the reference value. This can be prevented.
Because also of the reason the the D-part can be built with different approaches,
smoothed or as difference to older values,
the PID*Ctrl_emC has an extra input for the difference named dx
and an associated Parameter dt for the step time spread of this dx.
You can decide how the D-part is built. smoothed or not, from w-x or only from -x.
3.4. Smoothing of the D part as necessary solution
If you have a exploration of a controlled system with pure mathematics, you can follow the theory on paper and pencil. If you have a simulation with a proper solver which solves near the physic (continues sample time) and double or also float arithmetic, you are near the mathematics. You get an behavior adequate to the mathematics.
But for real applications you have always defined fixed step times for controlling. The step times are often interrupts of a controller, and they can work only with defined times. In a simulation you can select also this fixed step times. The mathematics support that for example with the theory of z-Transformation.
But their is still another problem. Your calculation can be use float (or double) accuracy, but a measurement and actuators has anyway a defined and limited resolution. You can use an ADC (analog digital converter) with 16 bit resolution it it is possible but often only 12 bit are available. For fast measurements sometimes you get only 10 bit. Also an actuator has a limited solution, for example a pulse width modulation with a fast frame, but your controller has only a limited clock frequency.
If one have a sampled system with an integer measurement signal resolution, the changing of the input values from one to the next step are sometimes less with steps. This is typical, because the sampling rate of the controller should be high in comparison to the system behavior. If the change is less, the difference of change is also less or inaccurate. If the D part is immediately built with the difference of the inputs, then, because of the inaccuracy in fine solution, the D-part has a high noise. That is mostly disturbing.
Example: In a fast sample time (for example 50 µs for electrics or 1 ms for mechanical) you get an input signal which has a less growth or near zero. Then the ADC input switches from one value to the next as accident because of noise if the growth is near zero, or it switches in more as one sample times. For example your signal is changed from 50% to 51% for a mechanical system with 1 ms sampling rate in in 20 ms. If you have (only) 10 bit resolution, the measurement values are
500 | 500 | 500 | 501 | 501 |502 | 502 | 502 | 503 | 503 |504 | 504 . . .
As you see you have stages. The differential is
0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 . . . ----
On the other hand for stabilization it is necessary to regard very fast changes. That changes are a point of interest, which are in the time of the oscillating frequencies of the system, or the frequencies near the 0-dB crossing in the Bode Diagram (https://en.wikipedia.org/wiki/Bode_plot).
Often the necessary D-gain inclusively kP is a factor of for example 100.0 (Example kP = 5.0 and Td = 20* Tstep = 20 ms for the mechanical example). Then the D-Part in the output has shocks of 100, which is 10% of the output with the same as input solution. This is bad.
A floating point solution for all signals, near mathematical, is nice:
500.13 | 500.54 | 500.93 | 501.32 | 501.71 | 502.15 | 502.52 | . . . 0.xx | 0.41 | 0.39 | 0.39 | 0.39 | 0.44 | 0.37 | . . .
A little bit noise is shown, but the differential is stable ~ 0.4 and the output is a signal with this noise in range 37.0 .. 43.0 which is acceptable. The pure mathematics may not have noise.
One possible solution of that is: Combine the D-part with a smoothing. That is a general solution. One can set the smoothing time to 0, then the input of the D-part is immediately, not smoothed.
It is one stage harder: You should have a 2-step smoothing as the following examples as simulation results (which follows the reality) shows.
You can first build the D-part with the input differences, and afterwards smooth,
dx += fTDs * (dx - (x - xz)); xz = x;
but it is also possible to first smooth the input and then built the difference from the smoothed signal. The second one has the advantage that also the input value can be visited in smoothed form (data viewing).
dx = fTDs * (x - xs); xs += dx;
For the double smoothing twice smoothing from the input is used, from the second smoothing the addition part is the D-part:
Another possibility to build a smoothed D-part is: Using the current value and building the difference not with the immediate previous value, instead build the difference with a little bit more older value and divide by the number of values. This division increases immediately the resolution of the differential. Usage of an older value to build the difference is similar as smoothing: It result in a dead time. On smoothing it is a phase difference, or with another view, the smoothed value contains and depends from also the older values.
How is the smoothing of the D-part implemented?
Because there are at least two possibilities, and the differentiated signal may be built also with stuff outside, the Controller has an extra input for the differentiated value. So it can be decide outside how to build.
For smoothing there is a function block either T1f_Ctrl_emC as simple smoothing block
or even T2f_Ctrl_emC for a two-stage smoothing.
Both FBlocks have a dx data element useable as output.
The dx is related to the step time. It means it is the value of change in one step cycle.
Look on the implementation of this FBlocks:
=>source: src_emC/emC/Ctrl/T1_Ctrl_emC.c
static inline float step_T1f_Ctrl_emC(T1f_Ctrl_emC_s* thiz, float x) {
thiz->dx = (thiz->fTs * ( x - thiz->q)); //
thiz->q += thiz->dx;
return thiz->q;
}
static inline float get_dx_T1f_Ctrl_emC(T1f_Ctrl_emC_s* thiz) {
return thiz->dx; //regard step is executed before!
}
static inline float step_T2f_Ctrl_emC(T2f_Ctrl_emC_s* thiz, float x) {
float dx1 = (thiz->fTs1 * ( x - thiz->q1)); //
thiz->q1 += dx1;
thiz->dx = (thiz->fTs2 * ( thiz->q1 - thiz->y)); //
thiz->y += thiz->dx;
return thiz->y;
}
static inline float get_dx_T2f_Ctrl_emC(T2f_Ctrl_emC_s* thiz) {
return thiz->dx; //regard step is executed before!
}
You see the two stage smoothing. Follow the results in the after-next chapter.
The other possibility is using a simple delay FBlock Delayf_Ctrl_emC.
This FBlock stores data values in a ring buffer and returns a requested earlier value.
Building the difference between the current and the returned earlier value is the differential.
This differential is related to the delay time.
It means the value is greater as for using the smoothing block.
To prevent additional effort for dividing (multiply with a constant)
this is regarded in the parameterizing of the PID controller.
=>source: src_emC/emC/Ctrl/T1_Ctrl_emC.c
/**Get the delayed value of a input in the past, put the new value for delay.
* This routine should only be called one time per step time.
* @param delay number of step times to the past for the output
* @param x the new input
* @return the value from past due to delay.
*/
INLINE_emC float step_Delayf_Ctrl_emC ( Delayf_Ctrl_emC_s* thiz, int delay, float x ) {
#ifndef __ignoreInCheader_zbnf__
ASSERT_emC(delay >0 && delay < thiz->nsize, "faulty delay value", delay, thiz->nsize);
int ixold = thiz->ix - delay + 1;
if(ixold <0) { ixold += thiz->nsize; }
float val = thiz->values[ixold];
int ixnew = thiz->ix +1;
if(ixnew >= thiz->nsize) { ixnew = 0; } // wrap arround 0
thiz->ix = ixnew;
thiz->values[ixnew] = x;
return val;
#endif//__ignoreInCheader_zbnf__
}
3.5. Measurements with D-Part
To see real test results, follow the next curve. It is executed by the same algorithm as the integrator wind-up test. Here the D-part is activated, which reduces oscillation. The following controller parameter are used on the same environment parameter:
see source in Test_emC/src/test/cpp/emC_test_Ctrl/test_PIDf_Ctrl.c float xquant = 20000.0f; // build input signal with this ADC resolution (quantization) int ndxDelay = 1; // 0: smooth D-part, 1..31 use delayed values float td = ndxDelay ==0 ? Tctrl : ndxDelay * Tctrl; float Tsd1 = 0.000200f, Tsd2 = 0.000200f; //time only for smoothed D-input float kP = 30.0f, Tn = 0.005f, Td = 0.00100f; float fT1 = 0.01f, fT2 = 0.05f, fT3 = 0.1f; //Ts = 5 ms, 1 ms, 0.5 ms int bonly_xdx = 0; // select, use x or w-x for D-part.
In comparison to the solution without D-part, the P-gain (kP) is higher, 30.0 instead 4.0,
because the instability without D-part is solved by the damping effect of the D-part.
The D-part has no smoothing, but the resolution of the input signal is +/- 20000,
adequate to an ADC bit width of 15 bit.
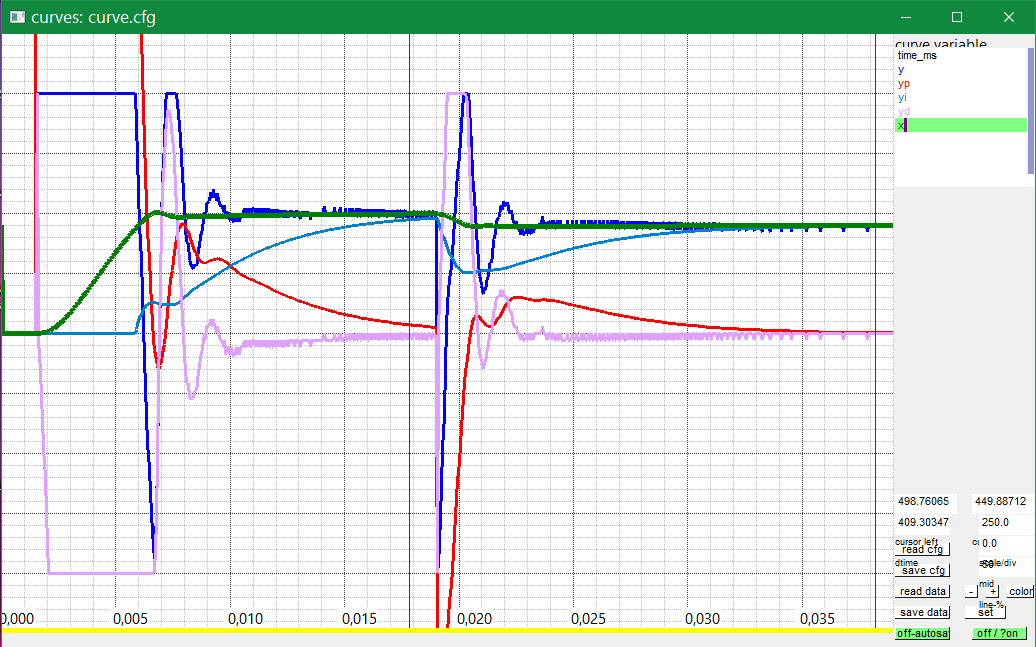
The environment output x (green curve) is fast towards the end value,
very more better than without D-Part. There is only a little bit overdrive.
The overdrive is seen on the P-part (proportional to the controlling error wx,
but with the P-gain, here 30.0) which is near the 0.
This is also true on the non limited step response from 0.5 to 0.4 right side.
The D part is the violet curve. First, it goes in the same direction as the P-part because of the rising reference value. But after a small time, the rising of the input x value forces a negative value till max. But both are not effective because the controlling error forces a high P part till limitation. Hence also the integrator is hold, and the reaction of the system is firstly the same.
The controller output lefts the max value on an earlier time , because the negative D-part forces this limitation-left already on P-part = 2.0, not only on 1.0 because the D-part delivers -1.0. For this reason the integrator starts a little bit earlier which is also proper for the result.
The D-Part decreases the output (green) and the system stops changing. Then the output oscillates a little bit, and following the environment’s output x (red) goes in spurts to the final value. This is not so very nice, but it prevents the overflow of the output x (red) which may be necessary. The system itself is susceptible to vibration. That is the fact.
On the unlimited little step response in the mid you see the adequate behavior. Firstly the D-part goes in the direction of the step response, but then it follows changing of the x value. It damps the x value (red) which would be have elsewhere an overdrive.
You can also see a little restless in the D-Part and in the output. If you would use an only float simulation also for the input value this restless will be not seen. The float resolution is 24 bit, only on a large zoom it may be visible. If you use double - nothing. Such results from a theoretical exploration are proper to explain theory or maybe proper to offer a possible result, but they are not proper for practice.
The resolution of the input signal is programmed as:
float xEnvADC = ((int)(xquant*(xEnv)/valrange + 0.5f ) / xquant ) * valrange;
For the value quantization the expression
(int)(xquant*(wCtrl - xEnv)/valrange + 0.5f )
is essential. It converts the values to a range adequate xquant,
then removes the fractional part by building an integer. The valrange is 1000.0.
It is only necessary because of course the visible effect of the resolution
depends on the zoom for the curves and the used range of possible range.
The values for w are 500 and 450 to compare it with the interger version of PID,
it is the half of possible range for the resolution.
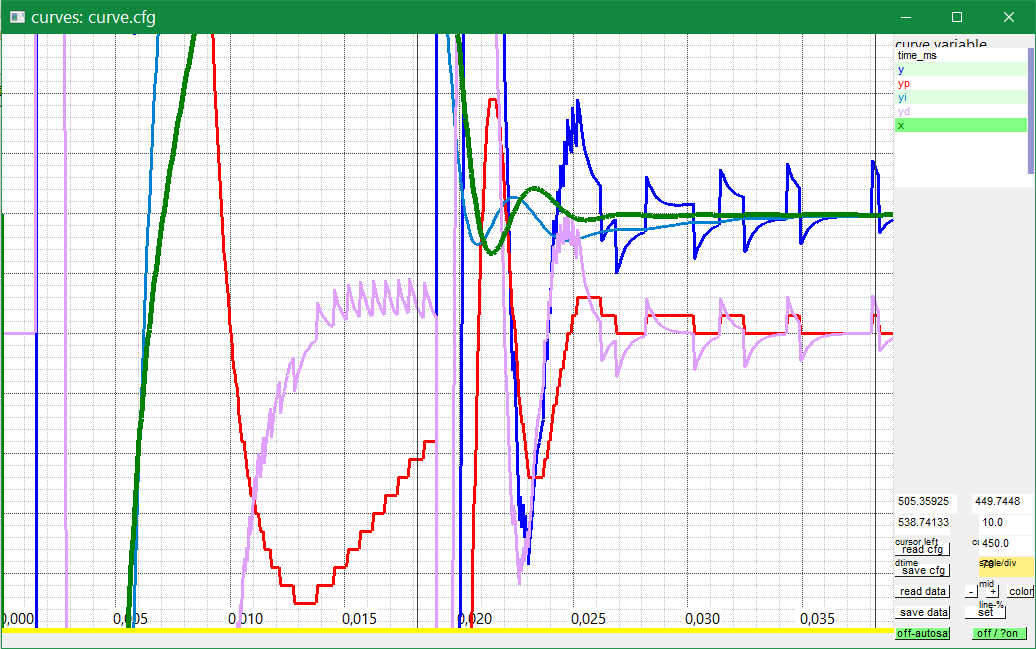
Now compare it with a resolution of 12 bit which may be familiar for some measurements. For a mechanical system it is a resolution of 0.5 mm for a spread of +/- 1 m.
The only one change is
float xquant = 2000.0f; // build input signal with this ADC resolution (quantization)
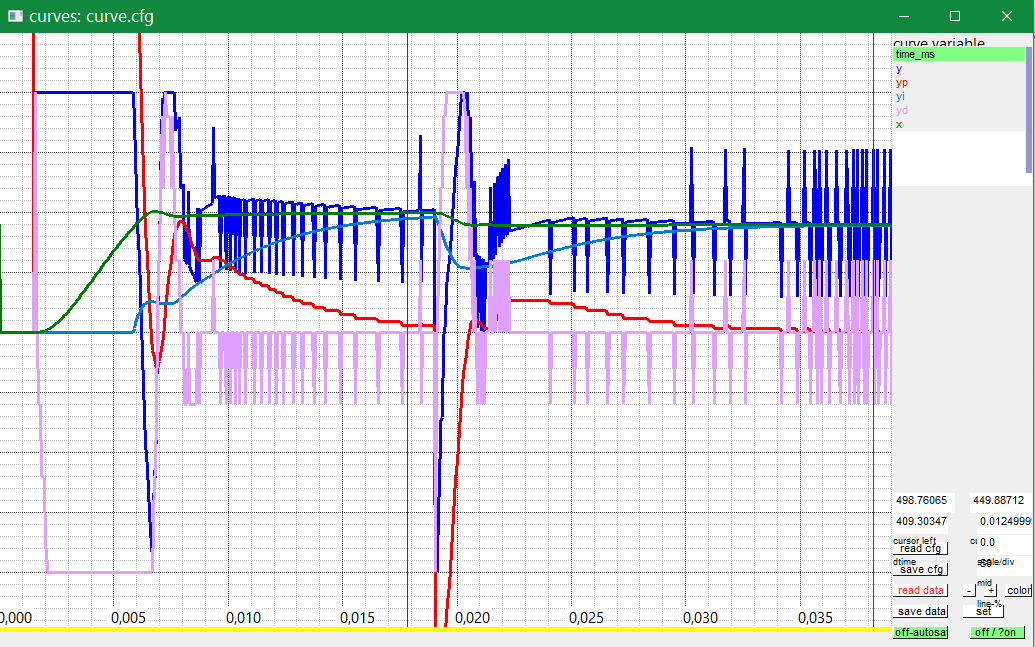
You see the resolution also in the P-Part (red) because for a gain of 30.0 the step width is 15.0 in the output by changing the input signal in one resolution step 0.5. The D-part is 'terrible'. Any step in input forces a change of D-part and output from 300, approximately a quarter of the output range, which is the result of the D-gain Td/Tctrl = 20. But, the output signal of the environment does not show this restless. It is filtered by the environment (a 3th order smoothing system). The restless is visible only on the output which is an actuator signal. This may be non acceptable.
Then compare it with smoothing of the D-part. The problem on smoothing is: The P-gain kP should be decreased and you get nevertheless more oscillation. This can be simple explained by a Niquist plot or also Bode plot. The phase angle is more worse, more near >180 degree, so the system get instable on higher gain. The same effect is occurring if you have a 4th smoothing time in your system.
float valrange = 1000.0f; float xquant = 2000.0f; // build input signal with this ADC resolution (quantization) int ndxDelay = 0; // 0: smooth D-part, 1..31 use delayed values float td = ndxDelay ==0 ? Tctrl : ndxDelay * Tctrl; float Tsd1 = 0.000200f, Tsd2 = 0.000200f; //time only for smoothed D-input float kP = 6.0f, Tn = 0.005f, Td = 0.001f; float fT1 = 0.01f, fT2 = 0.05f, fT3 = 0.1f; //Ts = 5 ms, 1 ms, 0.5 ms int bonly_xdx = 0; // select, use x or w-x for D-part.
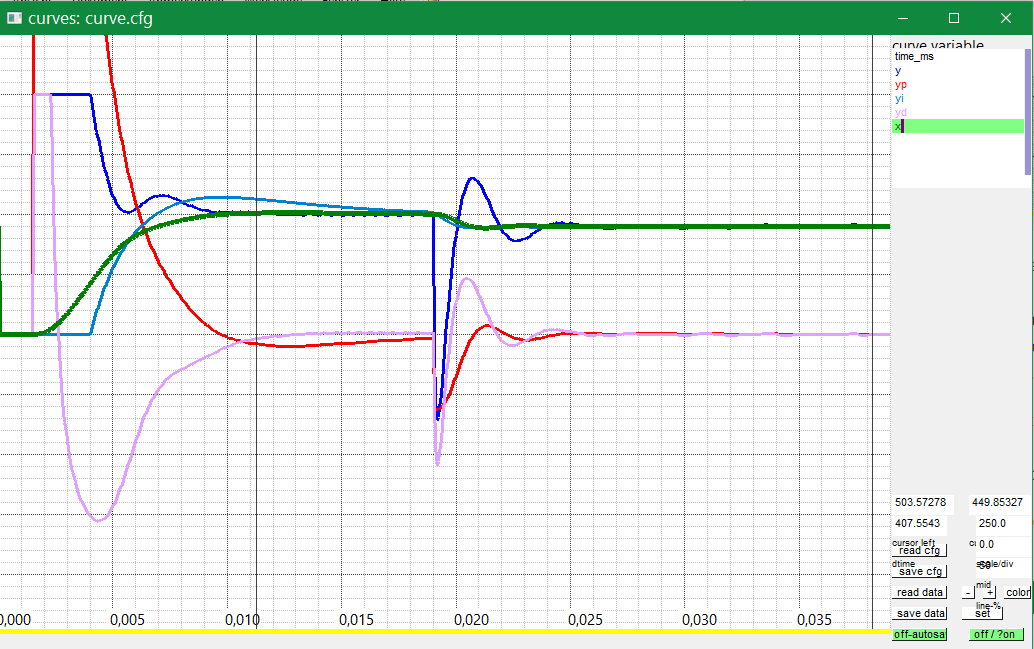
If you compare this result with the result without D-part, it is really better. If you compare with the higher resolved x input with higher gain, of course it is more worse, but it is the possible one. You see a little bit restless in the output, but only on exactly viewing.
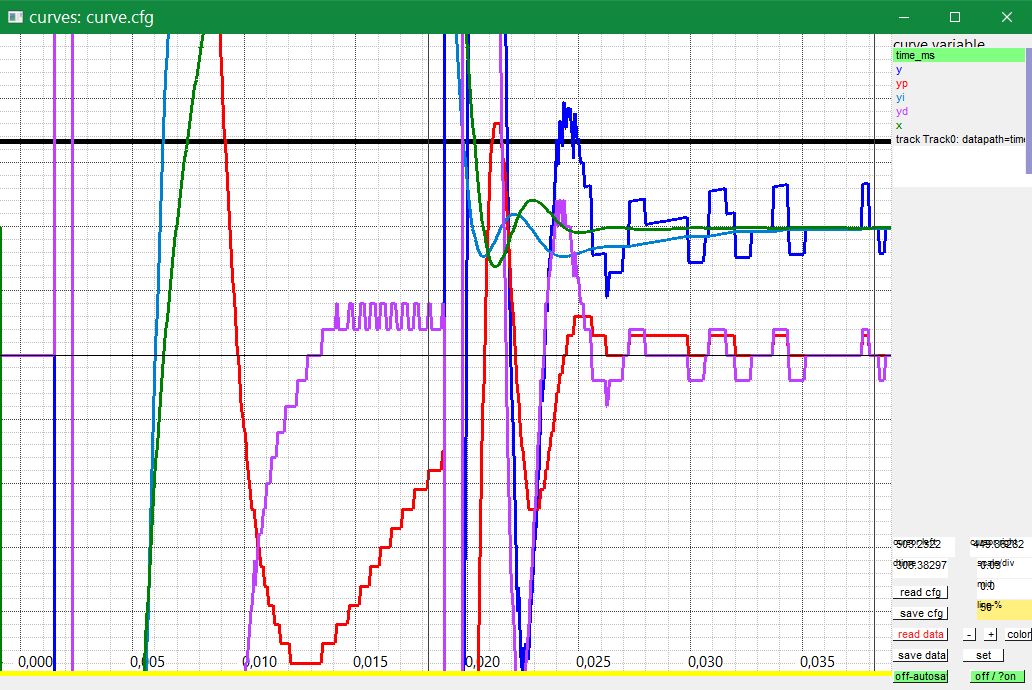
To see this a little bit more exactly, the zooming for D-part and P-Part are increased. The P part shows the measurement value in 0-level, as controlling error:

The scaling is 10.0/Div instead 250.0/Div, sorry the graphical tool CurveView is a little bit faulty.
The P-Part (red) is (w-x) * kP. Because kP=6.0 and the visible step size is 3.0,
the input x is quantized with 0.5. But the output is quantized because of the P-part
with this visible step of 3.0 because of kP. Additional the D-part is added.
This restless is 0.6% from the current value 500.0.
This is smoothed in the system,
on the system’s measurement signal you can only see a little bit movement
arround one step of the x input.
But the actuator is restless.
If you have a mechanical system, it is a restless movement around the current point.
This comes from the effect of resolution of the input with 12 bit.
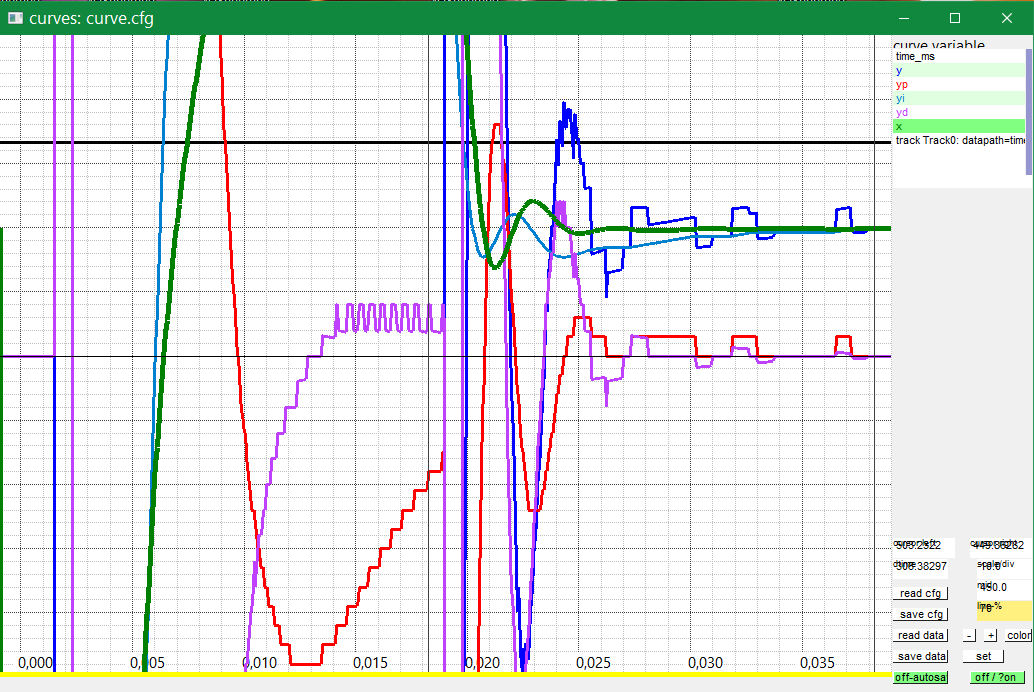
What is the result of a only one stage smoothing, with approximately double time:
float Tsd1 = 0.000000f, Tsd2 = 0.000450f; //time only for smoothed D-input
The osciallation is similar the same. But the D-Part and also the output signals has more hard shocks instead rounding shocks, of course result of the 2-stage smoothing.
In comparison to the non-filtered D-part: You have here as step response of the controlling error (red curve) an area with D-part value and the time. The area is the same as an only one impulse (dirac, https://en.wikipedia.org/wiki/Dirac_delta_function). But, of course, it is worn away in time.
Average:
Look on the result in smoothed form, the result without smoothing is really similar as above, The difference between the values is 12, hence the dead time is 6 Tstep or 0.3 ms for this example.
int ndxDelay = 15; // 0: smooth D-part, 1..31 use delayed values
The rest of the arguments are the same, he ndxDelay is used as:
float td = ndxDelay ==0 ? Tctrl : ndxDelay * Tctrl; ... init_Par_PIDf_Ctrl_emC(&thiz->parPid, 0.000050f, valrange, kP, Tn, Td, td, false, false); ... ... in step cycle: float xdxz = step_Delayf_Ctrl_emC(&thiz->delayx, ndxDelay, xdx);
The algorithm to built the smoothed differential can be seen as 'average of the differential from n points'. The disadvantage of this algorithm is: It needs memory for the possible number of points to build the average. Depending on the possible smooth time of ..16*Tstep. It needs 32 value buffer in this test example. More is not possible, or dynamic memory should be used.
Also here it is the same with the area of the step response to the changing of the controlling error. Instead a dirac impulse you get a square area with value * time with the same value. Note that the dirac impulse in a discrete time system is not infinitely high and zero-width, it has also an area with the appropriate high to the step time width.
Non-restless output in stable state
To get a non-restless output for example for a mechanical system it may possible to decrease the D-part on a less controlling error, respectively on reaching the end state. On electrical outputs (voltage converter) usual the voltage has not a static behavior, it is alternate current. The smoothed shocks in the actuator signal may be acceptable. The effect is filtered by chokes and capacitors in the electric circuit. But for that the rounded shocks may be better as hard shocks in a pulse width output.
To get an decreased D-part, you can use the FBlock
=>source: src_emC/emC/Ctrl/T1_Ctrl_emC.h
INLINE_emC float step_SmoothGainf_Ctrl_emC ( SmoothGainf_Ctrl_emC_s* thiz, float x, float gainhigh, float gainlow, float minx ) {
if (fabsf(x) < minx) {
thiz->gq += thiz->fTslow * (gainlow - thiz->gq); // smooth it down to gainlow
}
else {
thiz->gq += thiz->fTshigh * (gainhigh - thiz->gq); // smooth it down to gainlow
}
return x * thiz->gq;
}
The smoothing here is called with
dx = step_SmoothGainf_Ctrl_emC(&thiz->gains_dx, dx, 1.0f, 0.0f, 1.5f * valrange/xquant);
If you can see, the gain is decreased in a time if the value is below the xmin. This FBlock can also be used for a non linear controlling, for example to provide an higher gain on higher controlling error for a fast reaction.
The D part on the stable state becomes really lower. In following also the movement of the environment is lesser. One can also adapt such possibilities to the P-part. If you have really a less remaining error, the P-part can be lower.
Especially on a mechanical system with some stable end positions, this is a proper feature.
3.6. Building the D part only from the x value
The D-part is responsible to damping from view of the system’s or environment’s response, and it is similar responsible to force fast changes in direction of reference value changes. This may be interesting also on ramp stimulations.
But only seen for the aspect of damping, it is also sensitive to build the D-part
only from the environment response, not from the changing reference value.
That is supported by a special input of the controller to build the D-part,
named wxd. You can connect the same value as wx there then it is the standard behavior.
If you only connect the input of the controller (output of the system or environment) 'x'
then you have to negate it, use -x. Then you get in this example the following result:
float xquant = 2000.0f; // build input signal with ADC resolution (quantization)
float xEnvADC = ((int)(xquant*(xEnv)/valrange + 0.5f ) / xquant ) * valrange;
float wx = wCtrl - xEnvADC;
//step_PIDf_Ctrl_emC(&thiz->pid, wx, wx);
step_PIDf_Ctrl_emC(&thiz->pid, wx, -xEnvADC);
In comparison with the behavior using wx for the D-part
you have lesser oscillation of the controller output because the effect of w change is prevented.
But also the changing of the environment output 'x' is even lesser. Here you have no temporary overdrive, only damping.
It is a specific decision to decide because both possibilities.
The core algorithm of the controller supports both, without more effort
than the second input value.
The considerations of smoothing the D-part are the same.
4. Step times and operations
4.1. C or C++
The core algorithm are organized as C struct for the data
and as correspond C routines (extern "C" declaration in C++.
So it can be used in pure C environments.
There are wrapping C++ class definitions which allow a smart usage in C++
programming environments. The code overhead between C or C++ is exected as zero.
The wrapper are inline operations, which are expanded to the immediately C routine call.
Only the calling and data environment is adapted to C++ approaches.
4.2. Separation of parameter and control algorithm
It is important the the PID*_Ctrl_emC algorithm is executed also in a very fast time.
This is true also for the float variant (on more rich controllers) and the integer variants
for poor controllers. Hence focus on what is important in which time is necessary.
For example prevent a division in the fast step time though parameter may be changed given in natural units.
The PID control is generally divided into too parts with different data struct:
-
Par_PID*_Ctrl_emCcontains and prepares the parameter. -
PID*_Ctrl_emCcontains and execute the control algorithm.
That dispersion is also used because more as one PID*_Ctrl_emC for example
for more axis of a movement system can and should use the exact same parameter setting.
Only one instance of Par_PID*_Ctrl_emC should be exists.
Then also changing of parameters are exact similar effective.
The relation between both is an Aggregation (as in UML) from the PID*_Ctrl_emC
to its Par_PID*_Ctrl_emC, as simple ascii UML class diagram:
Par_PID*_Ctrl_emC <---<> PID*_Ctrl_emC
4.4. step: cyclically called
The step_PID*_Ctrl_emC(…) is that operation which should be executed unconditionally
in the controller cycle. This may be a 50 µs cycle for electric control.
Next this operation is completly shown (referenced from C file to this docu):
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
/**This is the core routine for PIDf ctrl, getting the built dx as value.
* It is static also to enable compiler optimization.
* @param wx Input for P and I
* @param dx Input for D-part as already built and smoothed differential
* @return y value.
*/
float step_PIDf_Ctrl_emC ( PIDf_Ctrl_emC_s* thiz, float wx, float dx)
{
ParFactors_PIDf_Ctrl_emC_s* f = thiz->par->f;
float wxP = wx * f->kP; //== P-Part
thiz->wxP = wxP;
float dxP = f->fD * dx; // effective D part for control with kP and Td/Tstep.
if (dxP > thiz->limf) { // limit it.
dxP = thiz->limf;
}
else if (dxP < -thiz->limf) {
dxP = -thiz->limf;
}
float y;
if(f->en ==0) { // if the controller is disabled,
thiz->yIntg = 0; // set integrator states to 0
thiz->qI.qI32 = 0;
thiz->yctrl = y = 0; // set the output to 0
// // but left thiz->wxP unchanged to view
}
else { // controller is enabled, calculate all P + I +D
y = wxP + dxP + thiz->yIntg + thiz->yAdd;
if(y >= thiz->limf) { // limitation necessary:
y = thiz->limf; // limit the output
if(thiz->qI.qI32 > 0x3F000000) {
thiz->qI.qI32 = 0x3F000000; // limit the integrator,
}
else if(thiz->qI.qI32 < -0x3f000000) {
thiz->qI.qI32 = -0x3f000000;
}
}
else if(y < -thiz->limf) { // same for negative limit
y = -thiz->limf;
}
else if(thiz->disableIntg ==0) { // integrate for next step only if not limited
int32 wxP32i = (int32)(f->fI * wxP); //growth for integrator
//Note: It is possible that a possible limitation was not detected just now,
//but it is effective in the next step time.
//Then the following is true:
//1) The max. value for qI32 in this moment is 0x3f00 correspond to fIy and fIx.
// An numeric overflow can never occur if Tn > 32 * Tstep (16 >= 0x7e00/0x01ff)
// That is a very less Tn, it is tested on parametrizing.
//2) An overdrive of the integrator for one step can occure
// because the integration is done after limit check.
// But this is only one time, only the integration of one Tstep.
// It is not effective for wind-up because it is integrated back
// in the next step time after left limitation.
ASSERT_TEST_emC(wxP32i <= 0x01ffffff && wxP32i >= -0x01ffffff, "overflow possible", wxP32i, thiz->qI.qI32 );
thiz->qI.qI32 += wxP32i; // use integer for exact integration.
thiz->yIntg = (int32)((thiz->qI.qI32)) * thiz->par->fIy; // float used.
}
else {
// // for test, manual changed yIntg is taken.
thiz->qI.qI32 = (int32)(thiz->par->fIx * thiz->yIntg); // Note: The I part is not limited
}
thiz->yctrl = y; // store output, after maybe limited
}
thiz->dxP = dxP; // store for viewing
//
//
if(!thiz->open) { // if the controller is losed, open loop only for test remains the y
thiz->y = y; // use the calculated for output
}
return y;
}
Of course also the D-part alone should be limited. Elsewhere it is possible especially on a large step response, that a negative D-part is added with a P-part the result is not limited, but the P-part is high positive and the D-part is highly negative.
The comment before integration is a hint of functionality on limits, which is asserted
by the ASSERT_TEST. This assertion is (should) only active in test situations.
The case is prevented, is never expected in runtime.
It has completely no impact to the calculation time in an application.
4.5. set_Par: Cyclically called in a slower thread or on demand
On demand means either in an event system, or with specific conditions.
A cyclically change of parameterization may be necessary if no parameter event is available. This is for example true in a standard Simulink environment or also on simple application solutions. But the changed parameters may be necessary not in the fast step time, can be done in a slower step time, or in a loopback with a maximal cycle time. It can be also called on demand. For cyclical call this routine checks first whether somewhat is changed. It calculates only newly on given changes:
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
/**set Parameter of PID controller
*/
void set_Par_PIDf_Ctrl_emC ( Par_PIDf_Ctrl_emC_s* thiz
, float kP, float Tn, float Td, float dt, bool reset ) {
bool bChanged = false;
//man=1 is used to change the values direct with Inspector
if( thiz->man == 0
&& ( thiz->kP != kP || thiz->Tn != Tn || thiz->Td != Td || thiz->dt != dt
|| !(thiz->f->en) != reset
))
{ // if one of this is changed, then calculate newly.
thiz->kP = kP;
thiz->Tn = Tn;
thiz->Td = Td;
thiz->dt = dt;
bChanged = true;
}
if(thiz->man || bChanged) { //== calculate newly derived values only on change and notify the change.
ParFactors_PIDf_Ctrl_emC_s* f = &thiz->i[thiz->ixf]; //use the yet not active buffer of twice
f->en = reset? 0 : 1;
f->kP = thiz->kP; //A less value, especially 0 means "no integration" such as Tn very high.
f->fI = thiz->Tn <= 16*thiz->Tctrl ? 0 : thiz->fIx * (thiz->Tctrl / thiz->Tn);
//Note: Tn > 16*Tctrl because elsewhere an additional overflow check may be necessary in runtime.
//Tn is usual > 16*Tctrl.
ASSERT_emC(thiz->Tn > 16*thiz->Tctrl || thiz->Tn ==0, "", (int)(thiz->Tn/thiz->Tctrl), (int)(thiz->Tctrl * 1000000));
f->fD = thiz->kP * (thiz->Td / thiz->dt);
//fTsd is a value in range 0.000... 1.0
//
thiz->dbgct_reparam +=1;
thiz->f = f; // use this set complete immediately after calculation.
thiz->ixf = thiz->ixf==1 ? 0 : 1; // use the other one for next change of values.
}
}
In this routine a double buffer system is used. Firstly the new values are calculated
in a second not used buffer. Then this buffer is declared as current with on atomic operation.
The step_PIDf_Ctrl_emC(…) does never see inconsistent parameter values.
Here the ASSERT_emC can be left active also in runtime. It is not a ASSERT_TEST_emC.
It needs a little bit time to check but not to calculate the additional values to show
because it is implemented as macro. If the user gives a faulty Ts, then a TROW occurs
which can be catched. This is possible also in a runtime application.
See chapter Assertion in Base/ThCxtExc_emC.html
Some more operations are existing which can also be called on demand, in an if condition, for only test conditions or never used:
4.6. reset_Par: Cyclically or on demand
A reset of a controller may be necessary for some operations, for example on the opened loop
if the loop is opened because physical conditions. For example a main breaker is not closed
for electric lines. Then the controller should be reseted by reseting of the parameter
using the set_Par_PIDx_Ctrl_emC(…) operation. You may not need new values for the parameter,
use the stored one. Use only the reset argument.
A reset can be given either with the set_Par_PIDf_Ctrl_emC(…) operation
see chapter above especially in a slower thread or in a background tassk,
or it can be given in the fast controller thread or interrupt by calling:
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
/**Reset or run all controller which are related to this parameter FBlock.
* This operation can be called in any thread.
* It takes effect on the next step_PIDf_Ctrl_emC(...) on all related controller.
* To combine reset with parameter values you can also use set_Par_PIDf_Ctrl_emC(...).
*/
INLINE_emC void reset_Par_PIDf_Ctrl_emC(Par_PIDf_Ctrl_emC_s* thiz, bool reset) {
thiz->f->en = reset? 0 : 1;
}
This routine is implemented as inline. It has less operations which can be better expand
in the current program than execute a call intruction.
A reset can also be given with the set_Par_PIDf_Ctrl_emC(…) operation above.
The controller parameter set has a en boolean element.
This is set either immediately with this reset_Par… routine or with a new parameter set
in the set_Par… routine or also initial via init_Par….
Hence you can determine both on startup and on new parametrizing whether all controllers
connected to one parameter set are reseted or enabled.
On reset the output of all controllers which are associated to this Par_PIDx_ctrl_emC
is set to 0, the integrator is set to 0 (important for enabling after)
and also the smoothing of the differential is cleared. So on eabling the controller
starts with a smoothed differential and 0 for the integrator.
You can change the output by setting the variable yAdd in the struct
either manually by the Inspector tool or with a special part in the software.
This is only thought for debugging.
4.7. setLim: changing of the limits, cyclically or on demand
The limitation of the controller can be changed in the running state, for example if a following limitation condition occurs or the limitation of the more complex calculated output should be controlled. Note that the limitation value is symmetrically, and this value must be lesser or equal than the given maximal value on constructor.
If the limitation is never invoked, the maximal value on constructor is valid for that. The operation can be called conditionally. But it have to be executed in the same thread (interrrupt) as the step routine, because consistency of internal data.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
void setLim_PIDf_Ctrl_emC(PIDf_Ctrl_emC_s* thiz, float yLim) {
if(yLim > thiz->par->yMax) { yLim = thiz->par->yMax; }
else if(yLim <0) { yLim = 0; }
if(yLim < thiz->limf) { //== check the integrator only on lesser limit
//note: on increasing the integrator is never faulty. Save calc time.
if(thiz->yIntg > yLim) { // limit the integrator if it is now out of limit
thiz->qI.qI32 = (int32)(thiz->par->fIx * yLim);
thiz->yIntg = yLim;
} else if(thiz->yIntg < -yLim) {
thiz->qI.qI32 = -(int32)(thiz->par->fIx * yLim);
thiz->yIntg = -yLim;
}
}
thiz->limf = yLim; // now set it!
}
Here the strategy "correct a violate design by contract, don’t report it" is used. It is adequate because the value of the limit should of course be appropriate to the given ranges. A faulty too high limit value is replaces with the maximum, a deficient behavior is prevented.
4.8. setIntg: changing of the integrator value, cyclically or on demand for special cases
This operation can also be used only in special cases, for example
if a proper value for the integral part is saved before, and the state should be recovered.
Here also a faulty value for intg is simple limited to an admissible value.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
void setIntg_PIDf_Ctrl_emC(PIDf_Ctrl_emC_s* thiz, float intg, bool set, bool hold, float* intg_y)
{
if(set) {
if(intg > thiz->limf) { intg = thiz->limf; }
else if(intg < -thiz->limf) { intg = -thiz->limf; }
thiz->yIntg = intg;
int32 qI = (int32)(thiz->par->fIx * intg); // set I part, convert float to int32
thiz->qI.qI32 = qI; // Note: The I part is not limited
thiz->setIntg = 1;
thiz->disableIntg = 1;
} else {
thiz->setIntg = 0;
thiz->disableIntg = hold;
}
if(intg_y !=null) { *intg_y = thiz->yIntg; }
}
4.9. Construction and init
In the correct order this operations should be named firstly. But often the user may firstly interest on the step routine. The ctor and init is executed only one time.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
Par_PIDf_Ctrl_emC_s* ctor_Par_PIDf_Ctrl_emC(ObjectJc* othiz, float Tstep)
{ //check before cast:
ASSERT_emC(CHECKstrict_ObjectJc(othiz, sizeof(Par_PIDf_Ctrl_emC_s), refl_Par_PIDf_Ctrl_emC, 0), "faulty ObjectJc",0,0 );
Par_PIDf_Ctrl_emC_s* thiz = (Par_PIDf_Ctrl_emC_s*)othiz;
return thiz;
}
The constructor for the parameter is widely empty. The assertion can be remain active also in the target system, it is only checked one time and needs hence only ROM space, but it detects a maybe memory error if the software was quickly changed and hence sometimes dirty.
The initialization with the ObjectJc* othiz argument which should refer the whole data
and returning the correct pointer, after assertion test, is an emC convention, see
chapter Initializing in ObjectJc_en.html
The variable Tstep is not used. It is especially for Simulink S-Functions as information for the Sfunction wrapper about the step time of the step function if the step time is no elsewhere defined. It is a non-tunable parameter of the S-Function.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
PIDf_Ctrl_emC_s* ctor_PIDf_Ctrl_emC(ObjectJc* othiz, float Tstep)
{
//check before cast:
ASSERT_emC(CHECKstrict_ObjectJc(othiz, sizeof(PIDf_Ctrl_emC_s), refl_PIDf_Ctrl_emC, 0), "faulty ObjectJc",0,0 );
PIDf_Ctrl_emC_s* thiz = (PIDf_Ctrl_emC_s*)othiz;
//should be done outside! CTOR_ObjectJc(othiz, othiz, sizeof(PIDf_Ctrl_emC_s), refl_PIDf_Ctrl_emC, 0);
//inner ObjectJc-based struct:
//CTOR_ObjectJc(&thiz->f.base.obj, &thiz->f, sizeof(thiz->f), refl_ParFactors_PIDf_Ctrl_emC, 1);
thiz->Tstep = Tstep; //park it here.
return thiz;
}
This is the constructor of the controller itself adequate to the parameter constructor.
But this constructor stores the given Tstep
temporary (in thiz→yctrl) to compare it with the given Tctrl on parametrizing.
The both constructors should be firstly executed on startup before init.
Both expects a basic initializing of the ObjectJc base structure.
The ObjectJc base data contains some information depending on settings
see ../Base/ObjectJc_en.html. The construction of the ObjectJc basic data
should be done on the creation of the instances, for example as static in C
with the INIZ… macro, see example:
typedef struct DataAll_T {
PIDf_Ctrl_emC_s pid;
Par_PIDf_Ctrl_emC_s parPid;
} DataAll;
#define INIZ_DataAll(THIZ) { \
INIZ_PIDf_Ctrl_emC(THIZ.pid, 0) \
, INIZ_Par_PIDf_Ctrl_emC(THIZ.parPid, 0) \
}
For C++ usage this is done in the {c++} constructor, see
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
#if defined(DEF_cplusplus_emC) && defined(__cplusplus)
class Par_PIDf_Ctrl_emC : public Par_PIDf_Ctrl_emC_s {
/**Constructs.
*/
public: Par_PIDf_Ctrl_emC (int idObj, float Tstep, float yNom ) {
CTOR_ObjectJc(&this->base.obj, this, sizeof(Par_PIDf_Ctrl_emC_s), refl_Par_PIDf_Ctrl_emC, idObj); //should be initialized.
ctor_Par_PIDf_Ctrl_emC(&this->base.obj, Tstep); //the initialized ObjectJc as arguement.
}
This can be adequate done also on dynamic allocation in C.
The init operatios should be executed after construction.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
bool init_Par_PIDf_Ctrl_emC(Par_PIDf_Ctrl_emC_s* thiz, float Tctrl_param, float yMax_param
, float kP, float Tn, float Td, float dt, bool reset, bool openLoop_param)
{ //check before cast:
thiz->Tctrl = Tctrl_param;
thiz->yMax = yMax_param;
thiz->fIy = thiz->yMax / (float)(0x78000000L);
thiz->fIx = (float)(0x78000000L) / thiz->yMax; //for yMax the value is 0x78000000 no overflow because limitation.
thiz->i[0].open = thiz->i[1].open = openLoop_param ? 1 : 0;
thiz->ixf = 0; // set to i[0] to first usage
thiz->i[0].en = reset? 1 : 0; //set to no reset, to detect anyway first change!
set_Par_PIDf_Ctrl_emC(thiz, kP, Tn, Td, dt, reset); //note: initializes f := i[0]
setInitialized_ObjectJc(&thiz->base.obj);
return true;
}
The init operation of the parameter does not need any other information.
Hence it is finished unconditionally (return true)
and sets is initialized status setInitialized_ObjectJc(&thiz→base.obj);.
Before that all parameter are calculated. The set_Par_PIDf_Ctrl_emC(…) routine
is executed one time, see chapter above: set_Par: Cyclically called in a slower thread or on demand.
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.c
bool init_PIDf_Ctrl_emC(PIDf_Ctrl_emC_s* thiz, Par_PIDf_Ctrl_emC_s* par) {
bool bOk = (par != null && isInitialized_ObjectJc(&par->base.obj)); //paramter should be already initialized
if(bOk) {
ASSERT_TEST_emC(par->f !=null, "f should be set", 0, 0);
thiz->par = par;
// // compare Tstep stored in yctrl with par->Tctrl, should be the same
ASSERT_emC(par->Tctrl == thiz->Tstep, "faulty Tstep", (int)(par->Tctrl * 10000000), (int)(thiz->yctrl*1000000));
//It cleans only a bit. The rest is done in another time slice.
thiz->limf = par->yMax; // initial value for limf, if setLim_PIDf_Ctrl_emC is not called
thiz->disableIntg = thiz->open = par->f->open ? 1 : 0; //hint: f->open is only determined initially.
setInitialized_ObjectJc(&thiz->base.obj);
}
return bOk;
}
For using see chapter Construction and initialization in startup.
5. Data and its consistency
Per se, the question to the data should be presented firstly before the operations.
"Tell me what data you have and then I know who you are".
The private encapsulation of data is proper for software access order, data should only be changed by its operations. But exactly because of the speach above, data are presented also in the class view of UML diagrams.
5.1. PIDf_Ctrl_emC
Look firstly on the data of the controller itself:
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
/**Main data of PID controller
* @simulink no-bus.
*/
typedef struct PIDf_Ctrl_emC_t
{
union { ObjectJc obj; } base;
/**Aggregation to parameter. */
Par_PIDf_Ctrl_emC_s* par;
/**Current limitation of output (state). */
float limf;
/**Smoothed differential (state). */
float xds, xds2;
float wxavgbuf[32];
int ixAvg;
float wxavgSum, wxavgSum0;
/**Non limited P part kP*wx. Interdediate value, not a state. */
float wxP;
/**Stored for D-part, to view input. Interdediate value, not a state. */
float dxP;
/**float representation for the integrator (state if disableIntg). */
float yIntg;
/**To view the control output in open loop state. Interdediate value, not a state. */
float yctrl;
/**Value of the integrator (state). @boundary 8. Useable with 64 or 32 bit. */
union { int64 qI64; int32 qI32; } qI;
int8 setIntg, disableIntg, open;
int8 _sp_[1]; //at least 8 bit boundary
/*A space for a adding value maybe referred manually by pyAdd. */
float yAdd;
/**The current output of the controller, hold if open is set. */
float y;
/**This value is only set in construction, should inform about the step time. */
float Tstep;
} PIDf_Ctrl_emC_s;
The data contains not only state variable (which should be stored and remembered).
It contains also some intermediate values which can be evaluated for internal view.
If you look on the graphical shown results in chapter Some implementation details this results can only be shown
because the access to the intermediate values are possible.
If the controller should be used on systems with really less data space,
a conditional compilation is given in the integer variants of the PIDi_Ctrl_emC,
valid for the whole application, see sources.
For controller which supports floating point operation
usual this less additional memory space is not a problem.
The meaning of the ObjectJc as base data is for data inspection, size check
and for the initializing state, see also ../Base/ObjectJc_en.html.
For the integrator, both 32 bit and 64 bit are preferred. The 64-bit-Variant can use exactly the same data, the same parameter set. The difference is only in the data width of the integration.
All data are aligned on a position which is able to divide by its size.
Thats why the position of the qI is tuned and commented
and a sp (spare) element is given.
It is not an disadvantage to do so, but it clarifies data images
for example if you get a data excerpt for debugging or tracing approaches.
The size of the data should always be divide by the sizeof(void*)
which also helps on data sorting, if the data size is not too small.
5.2. ParFactors_PIDf_Ctrl_emC
The data of the parameter has two parts. Firstly the prepared data for controlling.
In the step_PIDf_Ctrl_emC(…) operation only this data are used :
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
/**This struct contains the used factors for the PID control calculated from the parameters.
* It is an internal data struct used for message transfer of factors.
*/
typedef struct ParFactors_PIDf_Ctrl_emC_T {
/**Copied kP from input arguments. */
float kP;
/**Factor for D-Part including kP and Transformation to int32. */
float fD;
/**Factor for wxP for Integrator adding. used for 64 bit multiplication result.
* Note fix point multiplication */
float fI;
/**0=disable or reset, 1=enable.
* It is the negate reset argument of set_Par_PIDf_Ctrl_emC(..., reset); or reset_... */
int8 en;
/**Stored only initially for bout parameter sets */
int8 open;
/**Notify a change*/
int8 chg;
int8 _spare_[8/*sizeof(void*)*/ -3]; //alignment to sizeof(ptr)
} ParFactors_PIDf_Ctrl_emC_s;
How this values are calculated - see chapter set_Par: Cyclically called in a slower thread or on demand
5.3. Par_PIDf_Ctrl_emC
The data of the parameter FBlock contains two areas for the ParFactors_PIDf_Ctrl_emC
which are used as double or switch buffer on parameter changes.
The calculation of the factors with the changed values is firstly done
in the not used yet buffer. Afterwards the pointer f to the buffer is switched,
see also implementation of set_Par_PIDf_Ctrl_emC(… )
This assures data consistency, because the set_Par_PIDf_Ctrl_emC(… ) operation
is called usual in another thread. If this is not done,
intermediately the controlling may be faulty (instable or slow).
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
/**Parameter of PID controller
*/
typedef struct Par_PIDf_Ctrl_emC_T
{
union { ObjectJc obj; } base;
//union { uint32 v; Bits_Par_PIDf_Ctrl_emC_s b; } bits;
//union { uint32 i32;
//struct
//{
int8 ixf;
/**If set then changes from outside are disabled. For Inspector access. */
int8 man;
int8 _spare_[8/*sizeof(void*)*/ -3]; //alignment to sizeof(ptr)
int32 dbgct_reparam;
// };
// } bits;
/**for debugging and check: The used step time for calcualation of the factors. */
float Tctrl;
/**Maximal value for the y output. The integrator in the PID uses fix point 64 bit for high accuracy.
* This value is used to build the correct factors from float to fix point.
*/
float yMax;
/**Factor from float-x to int64 and to float-y-scale. */
float fIx, fIy;
/**Primary and used parameter: P-gain. */
float kP;
/**Primary parameter: Nachstellzeit. used: fI. */
float Tn;
float Td;
float dt;
/**Internal paramter depending factors. */
ParFactors_PIDf_Ctrl_emC_s* f;
ParFactors_PIDf_Ctrl_emC_s i[2];
//uint limPbeforeD: 1;
} Par_PIDf_Ctrl_emC_s;
5.4. C++ class data
The PID*_Ctrl_emC and the Par_PID*_Ctrl_emC are also presented as C++ class.
It is presented here only for the PIDf_Ctrl_emC, the Par… is similar:
=>source: src_emC/emC/Ctrl/PIDf_Ctrl_emC.h
#if defined(DEF_CPP_COMPILE) && defined(__cplusplus)
class PIDf_Ctrl_emC : public PIDf_Ctrl_emC_s {
/**Constructs.
*/
public: PIDf_Ctrl_emC (int idObj, float Tstep) {
CTOR_ObjectJc(&this->base.obj, this, sizeof(PIDf_Ctrl_emC_s), refl_PIDf_Ctrl_emC, idObj); //should be initialized.
ctor_PIDf_Ctrl_emC(&this->base.obj, Tstep); //the initialized ObjectJc as arguement.
}
/**Constructs as base class of any inherited controller.
* @arg objectJc forces calling CTOR_ObjectJc(...) in the inherited class ctor.
*/
protected: PIDf_Ctrl_emC ( ObjectJc* objectJc, float Tstep ) {
ctor_PIDf_Ctrl_emC(&this->base.obj, Tstep); //the initialized ObjectJc as arguement.
}
public: void init(Par_PIDf_Ctrl_emC_s* par) { init_PIDf_Ctrl_emC(this, par); }
public: void step ( float wx, float dx){ step_PIDf_Ctrl_emC(this, wx, dx); }
public: float y ( float wx){ return getY_PIDf_Ctrl_emC(this); }
};
#endif
The struct definitions have alwas the postfix _s
because the identifier without _s is preferred for the class name.
The class inherits all data of the struct and has no more own data.
It hasn’t also no virtual operations and also not a virtual destructor.
This is not necessary here. Virtual operations are sometimes not safe,
see also ../Base/VirtualOp.html. Hence the class data are exact equal to the struct data.
No additional effor in data.
All operations are presented by inlined class operations ('methods'). They call the C level functions. Also here no additonal effort. The code using C++ is exactly the same as C code.
But why using C++: For this approach it is better to read. You can write:
myData.pid2.step(wx, wx);
If you have a class instance myData with composites (nested instances) for the pid…,
one can use the pointer operator or use a reference. It is simple to read.
The machine code is the same. Instead in C you should write:
step_PIDf_Ctrl_emC(&myData.pid2, wx, wx);
Only you have the type designation in the name. This is an information for reading the source,
but this information can be gotten on viewing the pid2 element too,
and it decreases flexibility.
But look to the constructors, this is the difference. C has a simple approach to instantiate static data:
PID_Ctrl_emC_s mypid = INIZ_PID_Ctrl_emC(mypid, 0);
whereby INIZ_… is a macro for a proper initalizer list { … }.
This macro initializes especially the ObjectJc base data.
This is not possible in {c++}. If you want to create a static instance one can write:
PIDf_Ctrl_emC mypid(0, 0.000050f);
The invocation of the ctor_PIDf_Ctrl_emC() is no more possible in the application’s startup code,
instead it is executed in the automaticly application construction phase before reaching main.
That is not an disadvantage, but it is harder to debug.
If you set a breakpoint on main, the construction is already done.
The given sampling time (constructor parameter, 50 µs in the example) can also be a variable,
but it should be defined on static instantiation in a static way too.
That is because it is a construction argument.
If you have a class which contains some other classes, especially this controllers, the situation on static initialization of the whole composed class is the following:
class DataCpp {
PIDf_Ctrl_emC pid;
Par_PIDf_Ctrl_emC parPid;
public: DataCpp();
};
DataCpp::DataCpp()
: pid(123, 0.000050f)
, parPid(122, 0.001f, 12.0f)
{
}
DataCpp myDataCpp();
The situation is adequate. The constructor of the whole composed data are executed
before main() is reached. But you can set a breakpoint in the constructor.
The values for step times and limitation are given here as numbers,
because it is only one time in the application. But this numbers can also be defined
from another data source (with generated header) or from before given other static data.
Also constructor arguments are possible and may be recommended.
C++ is primary thought for a dynamic instantiation:
DataCpp* myDataRef;
void testCpp ( ) {
myDataRef = new DataCpp();
As you see now the constructor is executed in a routine which may or should be called
on startup time of the application after main().
You can use a heap in your embedded application only for startup allocations.
That may be a proper style guide. Hence you don’t need delete and destructors,
because the data are destroyed only on reset of the hardware.
But you can have also destructors if necessary.
The rest is adequate in C in C++. See also remarks for init_…
in chapter Construction and init
5.5. Data definition and initialization
You can also refer to ../Base/ObjectJc_en.html#initC.
5.5.1. Data Definition
There are two or three approaches to data definition:
-
a1) Static data one per instance (conventional in C, not recommended)
-
a2) Static data one struct with all instances for a whole component in the application. It means such as
typedef struct DataAll_T {
PIDf_Ctrl_emC_s pid;
Par_PIDf_Ctrl_emC_s parPid;
//... some more
} DataAll_s;
-
b) Using a heap for data and using allocation on startup.
The points a2) and b) are both proper for embedded applications. This is also true for C++ usage for the class variants, see chapter above.
If you use the static definition, a2) variant or similar also on a1)
you should have an initializer list which is a const expression in C.
The initializer list is applied to the static data as simple copy or 0-initialization
by the compiler. With the initializer list the instances are proper set
before the main(), the startup of the application is reached.
The initializer lists can be built with (example for the struct above):
#define INIZ_DataAll(THIZ) { \
INIZ_PIDf_Ctrl_emC(THIZ.pid, 0) \
, INIZ_Par_PIDf_Ctrl_emC(THIZ.parPid, 0) \
}
DataAll_s dataAll = INIZ_DataAll(dataAll);
If dynamic allocation is used for C language, a constructor for the Data_s
should be given, instead the INIZ_DATA(…):
static DataAll_s* ctor_DataAll(void* ram, int size) {
ASSERT_emC(size >= sizeof(DataAll_s), "size faulty", size, sizeof(DataAll_s));
DataAll_s* thiz = C_CAST(DataAll_s* ,ram); //== Initialize the members:
CTOR_ObjectJc( &thiz->parPid.base.obj, &thiz->parPid, sizeof(thiz->parPid), refl_Par_PIDf_Ctrl_emC, 0);
CTOR_ObjectJc( &thiz->pid.base.obj, &thiz->pid, sizeof(thiz->pid), refl_PIDf_Ctrl_emC, 0);
return thiz;
}
Now the data can be allocated and constructed with for example:
int sizeData = sizeof(DataAll_s); DataAll_s* thiz = ctor_DataAll(alloc_MemC(sizeData), sizeData);
For alloc_MemC see ../Base/MemC_Alloc.html.
You can also use a simple malloc(size).
If the `DataAll_s struct begins with an ObjectJc then you can also use
DataAll_s* thiz = ctor_DataAll(ALLOC_ObjectJc(sizeData, refl_DataAll, 123), sizeData);
5.5.2. Construction and initialization in startup
As chapter above, you may have static data.
Then it is initialized basicly with 0-values and the sizeof for ObjectJc.
If you have dynamic data, it is executed also on startup.
Generally the following approach is used:
startup:
-
execute all allocations with constructors or execute the constructors with given static data in C:
ctor_XYZ(...)
-
execute all init operations after construction in a while loop till all is ok:
//Example initializing on startup:
boolean allInit = true;
int catastrophicalcount = 100; //max. the number of instances
do {
allInit &= init_PIDf_Ctrl_emC(&data->pid1, &data->parPid);
allInit &= init_PIDf_Ctrl_emC(&data->pid2, &data->parPid);
allInit &= init_Par_PIDf_Ctrl_emC(&data->parPid);
} while (!allInit);
The init operation of the controller needs the aggregation to the parameter,
and it checks also whether the parameter are proper initialized.
This is one bit centralized in ObjectJc, see the concept in
../Base/ObjectJc_en.html#isInitialized.
This is a data dependency which is checked.
If the init_PIDf_Ctrl_emC(…) is called before init_Par_PIDf_Ctrl_emC(…)
it returns false and need a second call.
Even hence an initialization loop should be executed till all init… routines
returns true to the following schema:
If you have only a simple data dependency and a correct order, then this init loop is executed only one time. If the order is not proper as in this case, you need 2 loops. On mutual dependencies (not here) you need at least 2 loops, but a mutual dependency must not presume ready initialization by the other instance. The mutual dependency can only presume that another instance is given, complete for example an aggregation pointer, but the initializing should not be mutual. This will result in a deadlock. You can use data from a non ready initialized instance if that data are given by construction. If there is more complexity, you need a initialization in more stages.
Then startup is finished, the data are initialized and can work.
6. Some test possibilities
6.1. Open loop for the controller
Independent of the fact of reset, you can set a variable open in the PIDx_Ctrl_emC data
either initial by parameter of init_Par_PIDf_Ctrl_emC(…, bool openLoop_param)
or changed only manual by a debug tool on runtime.
If this variable is set, the controller output is stored in the element PIDx_ctrl_emC::yCtrl
so it can be viewed or tested, but the output of the controller in PIDx_ctrl_emC::y remains to its given value,
which is 0 on startup.
It means you can open the controller loop any time whereby the controller output is hold
in a maybe before found stable working point. Now you can make some tests.
If you close the controller afterwards, it remain working.
Such tests can also be done in practical use in a real physical environment.
But you should assure that the system is stable, no disturbing effects occur.
You can made such tests also for a limited time by an automatism.
The usual application for that is: Check the transmission function of the opened loop
to get results for stability estimation.
You can switch off the integrator by setting the disableIntg variable to 1
in the PIDx_Ctrl_emC data. Then the integrator does not go away on remaining wx inputs.
If you close the loop afterwards, the integrator was remaining on its proper value.
Then measurements are done without consideration of the I part.
You can also follow the program:
-
a) set
disableIntg = 1 -
b) Note the integrator value
-
c) open the loop by setting
open = 1 -
d) set
disableIntg = 0if the integrator part should be tested too. -
e) set
disableIntg = 1and set the noted integrator value of the stable state before. -
e) set
open = 0and thendisableIntg = 0to recover the closed state.
6.2. Disable the integrator
This is possible and necessary also as test case in a open loop szenario (see chapter above) else also for special tests in closed loop.
The variable disableIntg in the data struct of the controller can be set to non-zero,
then the integrator remains on the last current value.
You can change this value by a debug tool effective for the currently controller
by changing the variable yIntg. If you set disableIntg =0
then the integrator continues of course with this value.
7. The integer variant
Generally the integer variant of PIDi_Ctrl_emC works in the adequate way
with similar results as the float variant.
This chapter shows all data and algorithm and discusses differences and special integer solutions.
Generally, the integer variant is slower if the processor supports float artihmetic per hardware. Why it is so?
The integer variant should do some preparations to prevent numeric overflow. That are additional statements. The float arithmetic always normalizes all numbers per hardware, so that any numbers can be processed. With integer artithmetic this is not done, and non proper values causes errors. For example if the controlling error is large, and you have a large kP gain, then you get a very large value for the P part. This is not a problem for float. After the calculation you should anyway limit it, so the high P part is not a problem.
But for integer arithmetic, all numbers have their designated range. Designate a range for larger controlling errors on large P gain is not sensible, because it is anyway limited. To prevent an overflow with unexpected results on this not usable situation, it is necessary to check the input values, limit it, before the multiplication operation is executed.
That is an effort which is relative low for a slow processor with only fix point artihmetic but stupid for a fast float processor.
The integer variant of the PID control is sensible for cheap processors to execute it in a middle time, for example in a step time of 100 ms or ~ 1 ms, but never very more fast. Then using of integer is proper, it is faster.
7.1. Generally using INT_NUM_emC type for simple numeric
There are 16- or 32 bit controller. It is the width of the integer hardware arithmetic.
Usual it is also the register width.
But a 32 bit controller can also work usual with 16-bit register and memory access.
The next question is, how is the int type defined by the compiler.
In C and also C++ language the bit width of int is not determined,
it is usual the bit width of the CPU register.
But, some controller has 32-bit-arithmetic and define the bit widht of int
nevertheless with 16.
This ensures compatibility with often used older programs which uses this 16 bit-int definition.
Because of this undefined situation from view of an independent C/++ program the type
#define INT_NUM_emC int
is used. This should be defined in the compl_adaption.h
either as int or long or also as short for special test conditions
depending on the compiler definition for 'int'
and proper to the length of the arithmetic unit in the controller.
Adequate the value of
#define INT_NUM_NROFBITS 16
should be defined as 16 or 32 adequate to the defined type.
This type INT_NUM_emC is proper to use for the simple calculations to make it fast on the controller.
For the PID controller it is the type of inputs and outputs.
7.2. Decide using 16 or 32 bit for intermediate numbers
Independent of the bit width of INT_NUM_emC, for the PIDi_ctrl_emC
it can be decide to use 16 or 32 bit width int for the internal values of P and D.
Why?
If you use 16 bit int as input, and you have 12 bit as output width,
you have only 2 bits to fine-adjust a kP-value if you store the (kP * wx)
also in 16 bit. Follow the calculation example:
float kP = 1.25f; wx = 0x0400; //example for input y = 0x0480; //the correct output, 1.25 times, without overflow wxP = 0x1200; //intermediate result wx * fP, fP = 0x0005; //value of kP=1.25 as integer factor
The wxP = wx * fP is calculated in the example with 0x1200 = 0x0400 * 0x0005.
The wxP is limited to a max value of 0x2710,
because also the I and the D-part can have the same value, and the sum of all should not cause an overflow.
It means the number of bits for the intermediate result is not 16, it is only 14.
Hence the resolution of the kP part is limited to 0.25. This may be too inaccurate.
It the output has 14 bit, the kP resolution is limited to 1.0.
Hence, working with a 10 or 12 bit output gives the opportunity to have proper maybe sufficient kP resolutions, but a higher resolution of the output decreases the resolution of kP, if you have only 16 bit.
Calculating for addition or subtraction with 32 bit is not a high effort though the processor supports only 16 bit arithmetic. It needs two assembly statements using the carry flag and two 16-bit-locations (register) for the operands. The adaption from C/++ to the necessary machine code is well done by the compiler.
More as that, if your processor defines ìnt as 16 bit and you want to have it as normal numeric resolution,
but the controller has really a 32 bit arithmetic and registers, it will be stupid to use
only 16 bit for intermediate results.
That`s why the combination of 16 bit inputs and outputs and 32 bit intermediate values is very sensible.
You should define
#define INT_NUM_emC int
to use the native 16 bit int. Then on the PID controller you should use
the step32_PIDi_Ctrl_emC(…) operation which works internally with 32 bit intermediate values.
7.3. P part, kP resolution
The P part is built with a simple multiplication of the input value with the f→fP factor.
This is a 16-bit-with multiplication with 16 bit result for int16 as INT_NUM_emC type
and step16_…(…) for a 16 bit intermediate result:
//source: src_emC/Ctrl/PIDi_Ctrl.c[tag=step16P_PIDi_Ctrl_emC.c
int16 wxP; //== Build wxP in limited form, base for P + I + D
if(wx > f->wxlim) { // limit the input, should not cause overflow for kPi multiplication
wxP = f->wxlim * f->fP; // use the max. able to present value
} else if (wx < -f->wxlim) { // wxlim is ~ max int value/kPi
wxP = - f->wxlim * f->fP;
}
else {
wxP = wx * f->fP; //== P part mult can never overflow because checked against wxlim
}
The multiplication uses either a built in multiplication assembly statement
or a simple software emulation determined by the compiler.
As you see the input value is checked for limit before, see next chapter.
This prevents an overflow.
The resolution of the kP depends on the value range of the output.
If the output should have a full value range of 16 bit,
but the intermediate result of one part has only 14 bit (because p + I + D should be added),
then a f→kP = 1 means a kP of 4.0. This is because f→nShy = -2,
the output y can only be gotten left shifting the intermediate result of 14 valid bits.
That is not sufficient. It means for an output width of 16 bit an intermediate bit width of 32 bit should be used only.
But if the output has for example a range from +- 1000 which needs 11 bit,
it is sufficient to use 16 bit for internal calculation. The kP resolution is then 0.125
because the intermediate result is shifted to 3 bits to the right for the output.
That is usual enough for a typical application for simple embedded control.
If you use a 32 bit intermediate result, respectively 32 bit for the separated P, I and D part,
then you have a little, not large effort for a simple 16 bit processor,
but you calculates also the growth for the P part with a high resolution of kP.
You can use 16 or more bits for the output value, for example not as physical output
but as output in a cascade (as reference value for an internal controller).
That is done always independent of the defintion of INT_NUM_emC as 16 or 32 bit
if you use the step32_PIDi_CTrl(…) step routine.
7.4. Approaches for overflow, limitation, resolution
The integer variant has a possible overflow problem on multiplications. In the float variant you can multiply and afterwards limit. In the integer variant a non limited input can overflow with multiplication.
For float arithmetic you can calculate
y = kP * wx + I + fTd * dwx;
for any input value, also high controller error (wx) with a high kP part.
The controller output is limited of course, but afterwards.
If float is used, the intermediate results do not need limitation, the float range is proper.
But for integer arithmetic you may get overflows on multiplication results.
The proper solution to prevent that is: Check a limit for the input values,
depending on the parameterized fP and fD factor.
If the inputs are in a range, the multiplication do never overflow.
The pattern for that is:
int16 wxP; //== Build wxP in limited form, base for P + I + D
if(wx > f->wxlim) { // limit the input, should not cause overflow for kPi multiplication
wxP = f->wxlim * f->fP; // use the max. able to present value
} else if (wx < -f->wxlim) { // wxlim is ~ max int value/kPi
wxP = - f->wxlim * f->fP;
}
else {
wxP = wx * f->fP; //== P part mult can never overflow because checked against wxlim
}
How the wxlim should be calculated? It depends on the max admissible value for wxP.
The wxP has a resolution of 16 or 32 bit depending of the decision about intermediate value bit length,
see chapter above. But you cannot use the full range:
It should be regarded that P, I and D are calculated independently and sum afterwards. It means that the maximal value for the P part is not its native range, it is 1/3 or a little bit lesser because of possible integrator overflows which should also regarded.
A simple decision is: Using 10000 instead the theoretical 32767/3 ~ 10922.
for 16 bit width. That is 0x2710, or adequate 0x27100000 for a 32 bit intermediate result of P, I and D.
The I-Part can have a overdrive of (32767-30000) = 0x2767 or ~ 27% from 10000.
This overflow allows a factor for fI of 0.27, which is adequate to an Integration Time of 4 step times.
If you would use 10500 as nominal limit, you have a reserve for the Integrator
of (32767 - 31500) = 1267 which is 12.5% or an Integration Time of 8 step times which may be also proper.
For a given 16 or 32 bit width intermediate results, the calculation is done with:
float maxPIDf = 10000.0f * (1<<(thiz->numBits -16));
With them the
f->wxlim = (INT_NUM_emC)( maxPIDf / f->fP);
can be proper calculated, depending on a currently given kP gain.
This value is calculated firstly as float for calculation the integer factors
from the given natural float factors. This calculations can be done also from the compiler itself
using constexpr in C++.
Using this 16 bit resolution for the intermediate result, the output resolution is also limited
to this value, or 8191 (0x2000 … 0x1fff) if you need a full bit range output.
That is the limitation of a cheap and fast solution for a really poor 16 bit controller.
Using the 32 bit resolution for the intermediate result, you have a better resolution also for the output.
7.5. Bit width of the integrator is always 32 bit
A bit width of the integrator of 16 bit is anytime too less for proper operation. The integrator should use always 32 bit. Also on a 16 bit controller the necessary twice additions with carry can be emulated in software, which is already done by the C/++ compiler.
The range of the I part is not the full 32 bit range because it is added to P and D,
see last chapter. The maximual value of the I part is 0x31fdffff.
To prevent an overflow for the integrator, the following is done:
The maximal value of the P-part is the value of /- `0x2720xxxx` for 16- or 32 bit.
This is the input of the I-part to calculate the growth.
But the I part is only growing if the output is not limited.
The limitation check of the output is sufficient, because all three parts are not overdriven then.
But there is a remaining possibility that the P is near the limit for example positive,
the D is near the limit then negative, and the sum is not limited.
If this situation remains (not desirable), than the I part integrates till 2* the max value.
Then because of P + 2*I -D the limitation is reached and the integration stops.
It means the I-part need not be checked to overdrive, it is done already while checking the sum.
But the I-part has more as the twice range because its limits are `-0x80000000 ... 0x7fffffff`,
the limitation of output occurs at least at `- 0x2710xxxx`.
It means the integrator is stopped on max +- 0x4e200000.
The rest of the range is not used. It is away from the numeric overflow.
Look on the implementation if the I-part for 16 bit calculation
//source: src_emC/Ctrl/PIDi_Ctrl.c in step16_PIDi_Ctrl_emC(...)
int16 yI = (int16)(thiz->qI >> 16);// access hi 16 bit from qI
y = ((wxP + yI + dwxP) >> f->nShy);// output of P + I + D shifted to output range
if(y >= thiz->yLim) { // check limitaiton
y = thiz->yLim; // on limit do not integrate, hold the I-part
}
else if (y <= -thiz->yLim) {
y = -thiz->yLim;
}
else if(thiz->disableIntg ==0) { // only if output is not limited, integrate the I-Part.
int32 wxId; // nShKI is 0 in width range, only >0 for Tn >= 5000 * Tctrl
muls16_emC(wxId, wxP >> f->nShKI, f->fI); // growth for integrator in 32 bit width.
thiz->qI += wxId; // integrate
}
As you can see the calculation for the growth of the integrator is done
with a cheap 16 x 16 bit multiplication which’s result is 32 bit.
The used macro is defined either in emC/Base/Math_emC.h as
#define muls16_emC(R, A, B) { R = ((int32)(int16)((A) & 0xffff) * (int32)(int16)((B) & 0xffff)); }
With this definition the compiler may create proper simple assembly instructions for this approach
using only 16 bit register.
In C and also C++ the rule is given that only 32 bit inputs results in 32 bit.
Hence the additional casting.
Or this macro can be specific defined in the compl_adaption.h
using assembly instructions for specific processors for example with an additional multiply hardware.
7.6. Example of parameter
Following some ready to use parameter are shown for the fix point arithmetic for P and I, based on given floating point inputs in the left two columns. Also the result of P and y for one step is shown for an input of 1. It is also a test of the algorithm.
This results are produced with the following test:
//source: src/test/cpp/emC_Test_Ctrl/test_PIDf_Ctrl.c
/**This routine prints some results for kI and fI for the integer PID integrator. */
static void calcSomePIDiParam ( ) {
//Note: current dir is the IDE project dir
int sizeData = sizeof(Data_s);
Data_s* thiz = ctor_Data(alloc_MemC(sizeData), sizeData);
ASSERTs_emC(sizeof(thiz->pid) % sizeof(int64)==0, "size should be modulo long size for 8-byte-boundary", 0, 0);
ASSERTs_emC(sizeof(thiz->parPid) % sizeof(int64)==0, "size should be modulo long size for 8-byte-boundary", 0, 0);
float Tctrl = 0.001f;
ctor_Par_PIDf_Ctrl_emC(&thiz->parPid.base.obj, 0.002f);
ctor_PIDf_Ctrl_emC(&thiz->pid.base.obj, Tctrl);
ctor_T2f_Ctrl_emC(&thiz->dxs);
ctor_Delayf_Ctrl_emC(&thiz->delayx.base.obj, 20, sizeof(thiz->delayx) + sizeof(thiz->_delayxValues));
ctor_SmoothGainf_Ctrl_emC(&thiz->gains_dx.base.obj, 0.005f, 0, Tctrl);
float valrangeBitsiA[][2] =
{ { 1000.0f, 16}
, { 1000.0f, 32}
, { 10000.0f, 16}
, { 10000.0f, 32}
#if (INT_NUM_NROFBITS ==32)
, { 32767.0f, 16}
, { 32767.0f, 32}
, { 100000.0f, 32}
#endif
};
for(int ixrange = 0; ixrange < ARRAYLEN_emC(valrangeBitsiA); ++ixrange) {
float valrange = valrangeBitsiA[ixrange][0];
int bitsi = (int)valrangeBitsiA[ixrange][1];
#if (INT_NUM_NROFBITS ==16)
char const* sfoutm = "../../../src/test/out/Test_Ctrl/pidiParam16_%d_%3.0f.csv"; //"$TMP/pidiParam.csv";
#else
char const* sfoutm = "../../../src/test/out/Test_Ctrl/pidiParam32_%d_%3.0f.csv"; //"$TMP/pidiParam.csv";
#endif
char sfout[100]; sprintf(sfout, sfoutm, bitsi, valrange); //build file name
OS_HandleFile hcsv = os_fopenToWrite(sfout, false);
ASSERT_emC(hcsv !=null, sfout, 0, 0);
FILE* fout = getFILE_os_file_emC(hcsv); //fopen("d:\\vishia\\Java\\cmpnJava_vishiaGui\\src\\appl\\CurveView\\data2.csv", "wb");
float Td = 0;
int dti = 1;
float param[][2] = {
// kP Tn [ms] for Tctrl = 1 ms
{ 0.1f , 0.016f }
, { 0.2f , 0.016f }
, { 0.5f , 0.016f }
, { 1.0f , 0.016f }
, { 1.1f , 0.016f }
, { 2.0f , 0.016f }
, { 5.0f , 0.016f }
, { 10.0f , 0.016f }
, { 20.0f , 0.016f }
, { 1.0f , 0.001f }
, { 1.0f , 0.002f }
, { 1.0f , 0.003f }
, { 1.0f , 0.005f }
, { 1.0f , 0.020f }
, { 1.0f , 0.021f }
, { 1.0f , 0.022f }
, { 1.0f , 0.100f }
, { 1.0f , 1.0f }
, { 1.0f , 2.0f }
, { 1.0f , 10.0f }
, { 1.0f , 90.0f }
, { 0.2f , 0.05f }
, { 10.0f , 0.05f }
, { 0.2f , 50.0f }
, { 10.0f , 50.0f }
};
init_Par_PIDi_Ctrl_emC(&thiz->parPid32, Tctrl, (int)valrange, bitsi, 1.0f, 0.1f, Td, dti, false, false);
init_PIDi_Ctrl_emC(&thiz->pid32, &thiz->parPid32);
fprintf(fout, "bits numeric:%d; bits intermediate:%d; value range Y:%d= %8.8X, nShy=%d\n"
, INT_NUM_NROFBITS, bitsi, (int32)(valrange), thiz->pid32.yLim, thiz->parPid32.f12[0].nShy);
for(int ix = 0; ix < ARRAYLEN_emC(param); ++ix) {
float kP = param[ix][0];
float Tn = param[ix][1];
set_Par_PIDi_Ctrl_emC(&thiz->parPid32, kP, Tn, Td, dti, false);
reset_Par_PIDi_Ctrl_emC(&thiz->parPid32, true);
if (bitsi==16) { //cannot run step16 on 32 bit type
step16_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
} else {
step32_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
}
reset_Par_PIDi_Ctrl_emC(&thiz->parPid32, false);
if (bitsi==16) { //cannot run step16 on 32 bit type
step16_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
} else {
step32_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
}
//int fI16 = thiz->parPid16.f->fI;
//int fI32 = thiz->parPid32.f->fI;
fprintf(fout, "kP=%4.1f; Tn=%6.3f; nShP=%2d; kP=%4.4X; wxLim=%4.8X; shI=%2d; fI=%8.8X;"
, kP, Tn, thiz->parPid32.f->nShP, thiz->parPid32.f->fP, thiz->parPid32.f->wxlim
, thiz->parPid32.f->nShKI, thiz->parPid32.f->fI);
fprintf(fout, "P=%4.4X; I=%8.8X;\n"
, thiz->pid32.wxP, thiz->pid32.qI);
}
fclose(fout);
}
}
Look on the result for 16 bit intermediate results and an output range of 11 bit, till +- 1023:
//source: src/test/out/Test_Ctrl/pidiParam16_16_1000.csv bits numeric:16; bits intermediate:16; value range Y:1000= 000003E8, nShy=3 kP= 0.1; Tn= 0.016; nShP= 0; kP=0000; wxLim=00000000; shI= 0; fI=00001000;P=0000; I=00000000; kP= 0.2; Tn= 0.016; nShP= 0; kP=0001; wxLim=00002710; shI= 0; fI=00001000;P=0001; I=00001000; kP= 0.5; Tn= 0.016; nShP= 0; kP=0004; wxLim=000009C4; shI= 0; fI=00001000;P=0004; I=00004000; kP= 1.0; Tn= 0.016; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00001000;P=0008; I=00008000; kP= 1.1; Tn= 0.016; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00001000;P=0008; I=00008000; kP= 2.0; Tn= 0.016; nShP= 0; kP=0010; wxLim=00000271; shI= 0; fI=00001000;P=0010; I=00010000; kP= 5.0; Tn= 0.016; nShP= 0; kP=0028; wxLim=000000FA; shI= 0; fI=00001000;P=0028; I=00028000; kP=10.0; Tn= 0.016; nShP= 0; kP=0050; wxLim=0000007D; shI= 0; fI=00001000;P=0050; I=00050000; kP=20.0; Tn= 0.016; nShP= 0; kP=00A0; wxLim=0000003E; shI= 0; fI=00001000;P=00A0; I=000A0000; kP= 1.0; Tn= 0.001; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000000;P=0008; I=00000000; kP= 1.0; Tn= 0.002; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000000;P=0008; I=00000000; kP= 1.0; Tn= 0.003; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00005555;P=0008; I=0002AAA8; kP= 1.0; Tn= 0.005; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00003333;P=0008; I=00019998; kP= 1.0; Tn= 0.020; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000CCD;P=0008; I=00006668; kP= 1.0; Tn= 0.021; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000C31;P=0008; I=00006188; kP= 1.0; Tn= 0.022; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000BA3;P=0008; I=00005D18; kP= 1.0; Tn= 0.100; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=0000028F;P=0008; I=00001478; kP= 1.0; Tn= 1.000; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000042;P=0008; I=00000210; kP= 1.0; Tn= 2.000; nShP= 0; kP=0008; wxLim=000004E2; shI= 0; fI=00000021;P=0008; I=00000108; kP= 1.0; Tn=10.000; nShP= 0; kP=0008; wxLim=000004E2; shI= 2; fI=0000001A;P=0008; I=00000034; kP= 1.0; Tn=90.000; nShP= 0; kP=0008; wxLim=000004E2; shI= 5; fI=00000017;P=0008; I=00000000; kP= 0.2; Tn= 0.050; nShP= 0; kP=0001; wxLim=00002710; shI= 0; fI=0000051F;P=0001; I=0000051F; kP=10.0; Tn= 0.050; nShP= 0; kP=0050; wxLim=0000007D; shI= 0; fI=0000051F;P=0050; I=000199B0; kP= 0.2; Tn=50.000; nShP= 0; kP=0001; wxLim=00002710; shI= 4; fI=00000015;P=0001; I=00000000; kP=10.0; Tn=50.000; nShP= 0; kP=0050; wxLim=0000007D; shI= 4; fI=00000015;P=0050; I=00000069;
xxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
for the intermediate result as shown, ~ 1/3 of the integer range.
For a optimal calculation time only a 32 bit multiplication should be used, not 64 bit.
For an intermediate result of 16 bit, it is done with a simple cheap 16 x 16 ⇒ 32 bit multiplication
with the proper factor of fI. Look for an value example:
This overdrive can occure because firstly the limitation is tested and afterwards the integration is done. Near the limit the limitation is not detected and the growth is added to the integrator which is not extra tested. Hence the growth can be max 0xacf which is ~25% of the range. Hence the Integration time can be min 4*Tstep. See functionality of integrator.
Look for calculated examples of the fI and also the nShKI:
Tn=0.001000, shI16=0 fI16=0000, shI32=4 fI32=0010 Tn=0.002000, shI16=0 fI16=FFFF8000, shI32=5 fI32=0010 Tn=0.002100, shI16=0 fI16=79E8, shI32=6 fI32=001E Tn=0.003000, shI16=0 fI16=5555, shI32=6 fI32=0015 Tn=0.004000, shI16=0 fI16=4000, shI32=6 fI32=0010 Tn=0.005000, shI16=0 fI16=3333, shI32=7 fI32=001A Tn=0.007000, shI16=0 fI16=2492, shI32=7 fI32=0012 Tn=0.008000, shI16=0 fI16=2000, shI32=7 fI32=0010 Tn=0.015000, shI16=0 fI16=1111, shI32=8 fI32=0011 Tn=0.016000, shI16=0 fI16=1000, shI32=8 fI32=0010 Tn=0.030000, shI16=0 fI16=0889, shI32=9 fI32=0011 Tn=0.032000, shI16=0 fI16=0800, shI32=9 fI32=0010 Tn=1.000000, shI16=0 fI16=0042, shI32=14 fI32=0010 Tn=10.000000, shI16=2 fI16=001A, shI32=18 fI32=001A Tn=100.000000, shI16=5 fI16=0015, shI32=21 fI32=0015
The factors are based on a control Step time of 1 ms: Tctrl = 0.001f.
They are calculated with the algorith in Test_emC\src\test\cpp\emC_Test_Ctrl\test_PIDf_Ctrl.c
/**This routine prints some results for kI and fI for the integer PID integrator. */
static void calcSomePIDiParam ( ) {
//Note: current dir is the IDE project dir
int sizeData = sizeof(Data_s);
Data_s* thiz = ctor_Data(alloc_MemC(sizeData), sizeData);
ASSERTs_emC(sizeof(thiz->pid) % sizeof(int64)==0, "size should be modulo long size for 8-byte-boundary", 0, 0);
ASSERTs_emC(sizeof(thiz->parPid) % sizeof(int64)==0, "size should be modulo long size for 8-byte-boundary", 0, 0);
float Tctrl = 0.001f;
ctor_Par_PIDf_Ctrl_emC(&thiz->parPid.base.obj, 0.002f);
ctor_PIDf_Ctrl_emC(&thiz->pid.base.obj, Tctrl);
ctor_T2f_Ctrl_emC(&thiz->dxs);
ctor_Delayf_Ctrl_emC(&thiz->delayx.base.obj, 20, sizeof(thiz->delayx) + sizeof(thiz->_delayxValues));
ctor_SmoothGainf_Ctrl_emC(&thiz->gains_dx.base.obj, 0.005f, 0, Tctrl);
float valrangeBitsiA[][2] =
{ { 1000.0f, 16}
, { 1000.0f, 32}
, { 10000.0f, 16}
, { 10000.0f, 32}
#if (INT_NUM_NROFBITS ==32)
, { 32767.0f, 16}
, { 32767.0f, 32}
, { 100000.0f, 32}
#endif
};
for(int ixrange = 0; ixrange < ARRAYLEN_emC(valrangeBitsiA); ++ixrange) {
float valrange = valrangeBitsiA[ixrange][0];
int bitsi = (int)valrangeBitsiA[ixrange][1];
#if (INT_NUM_NROFBITS ==16)
char const* sfoutm = "../../../src/test/out/Test_Ctrl/pidiParam16_%d_%3.0f.csv"; //"$TMP/pidiParam.csv";
#else
char const* sfoutm = "../../../src/test/out/Test_Ctrl/pidiParam32_%d_%3.0f.csv"; //"$TMP/pidiParam.csv";
#endif
char sfout[100]; sprintf(sfout, sfoutm, bitsi, valrange); //build file name
OS_HandleFile hcsv = os_fopenToWrite(sfout, false);
ASSERT_emC(hcsv !=null, sfout, 0, 0);
FILE* fout = getFILE_os_file_emC(hcsv); //fopen("d:\\vishia\\Java\\cmpnJava_vishiaGui\\src\\appl\\CurveView\\data2.csv", "wb");
float Td = 0;
int dti = 1;
float param[][2] = {
// kP Tn [ms] for Tctrl = 1 ms
{ 0.1f , 0.016f }
, { 0.2f , 0.016f }
, { 0.5f , 0.016f }
, { 1.0f , 0.016f }
, { 1.1f , 0.016f }
, { 2.0f , 0.016f }
, { 5.0f , 0.016f }
, { 10.0f , 0.016f }
, { 20.0f , 0.016f }
, { 1.0f , 0.001f }
, { 1.0f , 0.002f }
, { 1.0f , 0.003f }
, { 1.0f , 0.005f }
, { 1.0f , 0.020f }
, { 1.0f , 0.021f }
, { 1.0f , 0.022f }
, { 1.0f , 0.100f }
, { 1.0f , 1.0f }
, { 1.0f , 2.0f }
, { 1.0f , 10.0f }
, { 1.0f , 90.0f }
, { 0.2f , 0.05f }
, { 10.0f , 0.05f }
, { 0.2f , 50.0f }
, { 10.0f , 50.0f }
};
init_Par_PIDi_Ctrl_emC(&thiz->parPid32, Tctrl, (int)valrange, bitsi, 1.0f, 0.1f, Td, dti, false, false);
init_PIDi_Ctrl_emC(&thiz->pid32, &thiz->parPid32);
fprintf(fout, "bits numeric:%d; bits intermediate:%d; value range Y:%d= %8.8X, nShy=%d\n"
, INT_NUM_NROFBITS, bitsi, (int32)(valrange), thiz->pid32.yLim, thiz->parPid32.f12[0].nShy);
for(int ix = 0; ix < ARRAYLEN_emC(param); ++ix) {
float kP = param[ix][0];
float Tn = param[ix][1];
set_Par_PIDi_Ctrl_emC(&thiz->parPid32, kP, Tn, Td, dti, false);
reset_Par_PIDi_Ctrl_emC(&thiz->parPid32, true);
if (bitsi==16) { //cannot run step16 on 32 bit type
step16_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
} else {
step32_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
}
reset_Par_PIDi_Ctrl_emC(&thiz->parPid32, false);
if (bitsi==16) { //cannot run step16 on 32 bit type
step16_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
} else {
step32_PIDi_Ctrl_emC(&thiz->pid32, 1, 0x0);
}
//int fI16 = thiz->parPid16.f->fI;
//int fI32 = thiz->parPid32.f->fI;
fprintf(fout, "kP=%4.1f; Tn=%6.3f; nShP=%2d; kP=%4.4X; wxLim=%4.8X; shI=%2d; fI=%8.8X;"
, kP, Tn, thiz->parPid32.f->nShP, thiz->parPid32.f->fP, thiz->parPid32.f->wxlim
, thiz->parPid32.f->nShKI, thiz->parPid32.f->fI);
fprintf(fout, "P=%4.4X; I=%8.8X;\n"
, thiz->pid32.wxP, thiz->pid32.qI);
}
fclose(fout);
}
}
As you see for Tn⇐0.002f, that is really extremely fast, it calculates bad results.
But from 0.0021f, it is also extremely fast, the results are proper.
The sensible range of Tn starts from ~ 32 ms, this is 32 step times, till ~ 100 seconds
which is extremely slow. For a controller which 1 ms step time,
an integration time in range of 100 ms till seconds is normally.
For the 16 bit intermediate result you can see that on 2.1 ms the 16 bit value for the P-Part is multiplied with a little bit lesser than 0x7fff, the greatest positive value, and the result is the half. That is correct. Look on the example:
wxP = 0x1e80; //a high P value f->fI = 0x79e8; //factor for TN = 1.2 ms, Tctrl = 1ms, =^ 1/2.1 f->NShKI = 0; //always for int32 wxId; muls16_emC(wxId, wxP >> f->nShKI, f->fI); // growth for integrator. It is 32 bit width maybe >0x10000. thiz->qI += wxId; // integrate, add 0x0e86
Also for 16 bit intermediate result a value of Tn=5.0 sec or from > 4.0 sec the P-Part is shifted to the right
which is a division by 2. Then it is multiplied with a value in the range 0x10..0x1f.
It means, depending on kP the importance of the last input bits becomes less, they are shifted out.
That is the effect that an remaining error is occured though the controller has a I part.
It is because the integration time is too high in comparison to the step time.
On the other hand the accuracy or better resolution of the Tn time is limited to 1/16 … 1/32. Using 5.1 ms results in the same `kI`as for 5.2 ms. If the resolution should be higher then the number of shifts should be greater, and hence the importance of the last bits will be lesser. That is the disadvantage of the simple using 16 x 16 bit ⇒ 32 bit for multiplication. But for normal usage in a poor controller that is not a meaningful disadvantage.
The 32 bit intermediate result for 16 bit input values (or lesser, 12 bit DAC or such) has native more bits, which presents a resolution with an accuracy which is not really given. Hence it is not so an problem to shift out for example 11 bits for Tn = 80 ms or 14 bit for Tn = 1.0 sec to multiply it afterwards with a factor with 4..5 bit resolution. The result is proper.
The value example for a 32 bit intermediate result is:
wx = 1; // 1 step change on input
//------------------------------------------------
int32 wxP; //== Build wxP in limited form, base for P + I + D
#if (INT_NUM_NROFBITS ==16)
f->nShP=8; f->fP=0x2800; // it is for kP=5.0 and INT_NUM_emC 16 bit width
muls16_emC(wxP, wx, f->fP); // results in 0x2800 <= 1 * 0x2800
wxP <<= f->nShP; // 0x00280000 <= 0x2800 <<8
#else
f->nShP=0; f->fP=0x00280000; // it is for kP=5.0 and INT_NUM_emC 32 bit width
mul32lo_emC(wxP, wx, f->fP); // (1 * 0x00280000) = 0x00280000
#endif // P part mult can never overflow because checked against wxlim
f->nShKI = 11; f->fI = 0x1a; //Tn = 80 ms on Tctrl = 1 ms, x/80 = (x>>11) * 0x1a
int32 wxId;
mul32lo_emC(wxId, wxP >> f->nShKI, f->fI); // growth for integrator. It is 32 bit width maybe >0x10000.
thiz->qI += wxId; //integrate 0x000`0'8200 <= (0x0000'0500 * 0x1a) <= (0x0028'0000 >>11) * 0x1a
For the kP part there is an additional distinction, whether the input value is 16 or 32 bit,
defined with the type INT_NUM_emC.
But both operations result in the value 0x0028'0000. This is the kP part.
Its distribution for the output depends on the shift for f→nSh32y which is 0x13 for this case.
The output value is only in range -1000…1000 which needs only 11 bits of the output.
It means for this calculated intermediate value for the P part the output is
(0x0028'0000 >>0x13) ⇒ 5 which is expected for wx = 1 and kP = 5.
The integrator takes this value, shifts it with 11 bits to right and gets 0x0500
in the 32 bit calculation.
For the 32 bit intermediate result, the result is first shifted to right with 7 bit, and then multiplied with
7.7. Parameter
As well for the float variant the following three data struct are defined:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.h
/**This struct contains the used factors for the PID control calculated from the parameters.
* It is an internal data struct used for message transfer of factors.
*/
typedef struct ParFactors_PIDi_Ctrl_emC_T {
/**Limitation of the input value wx (controlling error) to calculate the P part.
* This value is depending on fPi.
* It is calcualted that the range of P-part is at last < 1/3 from the INT_NUM_emC range.
* That is max. 10000 or max 655860000 for the P part.
*/
INT_NUM_emC wxlim; //new
INT_NUM_emC dxlim;
INT_NUM_emC fP;
/**Factor for D-Part including kP and Transformation to int32. */
INT_NUM_emC fD;
/**number of right shift from the intermediate representation (32 or 16 bit)
* for integration growth. */
int8 nShKI;
/**Number of right shift from the intermediate representation (32 or 16 bit) to the y output.*/
int8 nShy;
/**Number of right shift for wxP proper to fTs*/
//int8 nShfTs;
/**Number of right shift for wxP, (nShTD + nShfTD) == nSh32y */
//int8 nShTs;
/**Number of right shift for dwxP proper to fTD*/
//int8 nShfTD;
/**Number of right shift for yD, (nShTD + nShfTD) == nSh32y */
int8 nShP,nShD;
int8 en, open, _spare_[2];
/**Factor for wxP for Integrator adding. */
int32 fI;
} ParFactors_PIDi_Ctrl_emC_s;
That are the factors immediately used for control. As you see they are only integer values. As you can also see there are some values for shifting. This is necessary for integer arithmetic.
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.h
/**Parameter of PID controller
* @simulink bus.
*/
typedef struct Par_PIDi_Ctrl_emC_t
{
union { ObjectJc obj; } base;
/**Tstep of the controller, used step time for calcualation of the factors. */
float Tctrl;
/**Maximal value for the y output.
* This value is used to build the correct factors and bit shifts from float to fix point.
*/
INT_NUM_emC yMax;
//int xBits, yBits;
/**Primary and used parameter: P-gain. */
float kP;
/**Primary parameter: Nachstellzeit. used: fI. */
float Tn;
//float Tsd;
float Td;
/**Number of steps for the difference how the differential input is built.*/
INT_NUM_emC dt;
/**Bit width for internal multiplier for Tsd. Use at least 4 bits to assure a step width
* from 8..15. Use more bits for more solution of Td value. But do not use more than 8.
*
*/
int kBitTsd;
/**Internal paramter depending factors. */
ParFactors_PIDi_Ctrl_emC_s* f;
ParFactors_PIDi_Ctrl_emC_s f12[2];
/**If set then changes from outside are disabled. For Inspector access. */
uint8 man;
uint8 ixf;
uint8 numBits;
uint8 _spare_[8/*sizeof(void*)*/ - 3]; //spare till pointer size
} Par_PIDi_Ctrl_emC_s;
As you can see the given parameters are float values. You need on (re-) parameterizing float operations. But this is done either only on startup or in a really slow step time, so a float emulation can work.
If you have a really poor processor with low Flash memory, you can remove this data struct
and work only with the ParFactors_PIDi_Ctrl_emC_s data.
You should calculate the proper values outside of the controller and set it in this struct.
This can also be done by a second processor in the environment, or from a tool on PC,
or as only one initialization with compiler calculated values
(using for example the constExpr C++ facility).
Look on the algorithm how the used parameters are calculated:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.c
/**set Parameter of PID controller
*/
void set_Par_PIDi_Ctrl_emC(Par_PIDi_Ctrl_emC_s* thiz
, float kP, float Tn_param, float Td, int dt, bool reset) {
bool bChanged = false;
//man=1 is used to change the values direct with Inspector
if( thiz->man == 0
&& ( thiz->kP != kP || thiz->Tn != Tn_param || thiz->Td != Td
|| !(thiz->f->en) != reset
))
{ // if one of this is changed, then calculate newly.
thiz->kP = kP;
thiz->Tn = Tn_param;
thiz->Td = Td;
thiz->dt = dt;
bChanged = true;
}
if(thiz->man || bChanged) { //== calculate newly derived values only on change and notify the change.
MAYBE_UNUSED_emC int bitInt = 8*sizeof(INT_NUM_emC);
ASSERT_emC(thiz->Tctrl >0, "Tctrl <=0", (int)thiz->Tctrl, 0);
ParFactors_PIDi_Ctrl_emC_s* f = &thiz->f12[thiz->ixf]; //use the yet not active buffer of twice
//
f->nShP =0;
float maxPIDf = 10000.0f * (1<<(thiz->numBits -16));
if(thiz->numBits > INT_NUM_NROFBITS) { //== 32 bit internal calculation with 16 bit int
int maxfP = 1<<(INT_NUM_NROFBITS -2); // this is anytime 0x4000
int kPi = int(kP * 0x4 * (1 << (f->nShy -16))); // kP 1.0 =: 4
while( kPi !=0) {
f->nShP +=1; kPi >>=1; // shift 2 for kP = 1.0, shift 5 for kP = 8.0...15.999
}
f->fP = (INT_NUM_emC)(kP * (1 <<(16 - f->nShP + f->nShy -16))); // plays the role of a mantissa
float wxLim = maxPIDf / f->fP; // calculate input limit from fP
if(wxLim < (1<<(INT_NUM_NROFBITS-1))) {
f->wxlim = (INT_NUM_emC)( wxLim); // prevent numerical overflow
} else {
f->wxlim = 0x7fff;
}
} else { //== 16 bit internal calculation with 16 bit int
f->fP = (INT_NUM_emC)(kP * (1 <<f->nShy)); // nr of fractional bits depends on nShy.
f->wxlim = (INT_NUM_emC)( maxPIDf / f->fP); // prevent numerical overflow
//
f->fD = (INT_NUM_emC)( (thiz->Td / thiz->Tctrl) * (1 <<f->nShy) / thiz->dt);
f->dxlim = f->fD ==0 ? (1LL<<(INT_NUM_NROFBITS-1))-1 : //max value of INT_NUM_emC
(INT_NUM_emC)( maxPIDf / f->fD); // prevent numerical overflow
}
// // Tn =0 should force no integration, Tn <= 2*Tctrl not admissible.
if(thiz->Tn <= 2* thiz->Tctrl) {
f->nShKI = 0;
f->fI = 0;
} else {
float kI = thiz->Tctrl / thiz->Tn;
int32 kI_intImage = *(C_CAST(int32*,&kI));
int16 kI_exp16 = kI_intImage>>16; // use 16 bit high part only for more optimization by compiler
int shKI = (0x3fff - kI_exp16) >>7; // use exponent from float presentation for shift. It is 5 for Tn = 16.1...32 * Tctrl
int shBits = shKI + 4; // get at least a resolution of 1/16 for Tn.
int32 nPmin = (1<< (f->nShy-4)); // The value in intermediate for resolution 1/16 of kP
//nPmin = (int32)(kP * nPmin); // it is greater if kP is greater
while ( (1<<shBits) < nPmin) { // so long as shBits are lesser, can increase resolution of Tn
shBits +=1;
}
//if(shBits < f->nShy-1) {
// shBits = f->nShy-1;
//}
//else
if(shBits < (32 - thiz->numBits)) { //
shBits = (32 - thiz->numBits); // shBits = 0, no shift if kP is less. No shift for step16
}
f->nShKI = shBits - (32 - thiz->numBits) ; // necessary to get a fractional part
f->fI = (INT_NUM_emC)(kI * (1<< shBits) + 0.5f); //(1<<shBits) mults to 16..32
}
//
//thiz->dbgct_reparam +=1;
thiz->f = f; // use this set complete immediately after calculation.
thiz->ixf = thiz->ixf==1 ? 0 : 1; // use the other one for next change of values.
}
}
The first important values are xBits and yBits. They are given on construction.
it is the number of the bits for the input signals (wx, wxd) and the output signal y.
The input signal should not overflow the given number of bits, elsewhere the result is undefined.
For example if you have a 12 bit value from a ADC which is used immediately,
and also the reference value is in the same range, the number of bits for the input is 13.
It is not 12 because the max value of the ADC can be subtract with the min (negative) value of the reference.
The subtraction does never produce values outside. If you calculate it with int arithmetic,
also the padding of sign bits are correct. You can use 13 for xBits.
Adequate with the output. You should only use bits for the output which are defined by yBits.
For example you have a DAC output with 8 bit inclusively sign, 8 bit are enough.
If you have a PWM (PulsWidthModulation) with a conter range till max. 1023, 10 Bits are enough.
The internal accuracy is higher if you use lesser bits.
The problematic is always: Preventing overflow. Hence shift in correct ranges before arithmetic operations.
7.8. Step routine
The data are:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.h
/**Main data of PID controller
* @simulink no-bus.
*/
typedef struct PIDi_Ctrl_emC_t
{
union { ObjectJc obj; } base;
Par_PIDi_Ctrl_emC_s const* par;
/**Limitation value of y output. The output is never greater or lesser its negative equivalent.
* The I part will be limited too. */
INT_NUM_emC yLim;
INT_NUM_emC wx;
INT_NUM_emC wxd;
/**Stored smoothed P-Part, to view input and calculate D.
* It is possible that it is other normed. */
int32 wxds1, wxPs;
/**Only for view, current raw dwx related to wxPs norming.*/
int32 dwxPs;
/**Stored for D-part, to view input. */
//float wxPD;
INT_NUM_emC yD;
/**To view output. It is the same value as y_y arg of [[step_PIDi_Ctrl_emC(...)]]. */
INT_NUM_emC y;
/**Value of the integrator. */
int32 qI;
uint8 disableIntg;
#ifdef DEF_TestVal_PIDi_Ctrl_emC
INT_NUM_emC wxP;
INT_NUM_emC dxP;
#endif
/**Limited output from P and D fix point. To view. */
//int32 wxP32, wxPD32;
/**Value of the differentiator. */
//float qD1;
} PIDi_Ctrl_emC_s;
As you see, the integrator and the smoothing state variable are all `int32`. Others are `int` which is `int16` on a poor processor as its native.
Last look on the step16 operation:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.c
//Note: this routine is copied to RAM and runs in RAM in embedded target, sometimes faster.
RAMFUNC_emC INT_NUM_emC step16_PIDi_Ctrl_emC(PIDi_Ctrl_emC_s* thiz, INT_NUM_emC wx, INT_NUM_emC dwx)
{
ParFactors_PIDi_Ctrl_emC_s* f = thiz->par->f; //contains all parameter consistently
//Note: Limitation: Use 16 bit int for small processors and 32 bit int for larger.
INT_NUM_emC y;
int16 wxP; //== Build wxP in limited form, base for P + I + D
if(wx > f->wxlim) { // limit the input, should not cause overflow for kPi multiplication
wxP = f->wxlim * f->fP; // use the max. able to present value
} else if (wx < -f->wxlim) { // wxlim is ~ max int value/kPi
wxP = - f->wxlim * f->fP;
}
else {
wxP = wx * f->fP; //== P part mult can never overflow because checked against wxlim
}
//
#ifdef DEF_TestVal_PIDi_Ctrl_emC
thiz->wxP = wxP;
#endif
//
if(dwx !=0) {
dwx +=0;
}
// //== D-Part
int16 dwxP;
if(dwx >= f->dxlim) { // limit the input, should not cause overflow for kPi multiplication
dwxP = f->dxlim * f->fD; // use the max. able to present value
} else if(dwx <= -f->dxlim) { // limit the input, should not cause overflow for kPi multiplication
dwxP = - f->dxlim * f->fD; // use the max. able to present value
}
else {
dwxP = f->fD * dwx; //== P part mult can never overflow because checked against wxlim
}
#ifdef DEF_TestVal_PIDi_Ctrl_emC
thiz->dxP = dwxP; // store for viewing
#endif
// //== I-Part
if(f->en ==0) { // if the controller is disabled,
thiz->qI = 0; // set integrator states to 0
y = 0; // set the output to 0
// // but left thiz->wxP unchanged to view
}
else { // controller is enabled, calculate all P + I +D
int16 yI = (int16)(thiz->qI >> 16);// access hi 16 bit from qI
y = ((wxP + yI + dwxP) >> f->nShy);// output of P + I + D shifted to output range
if(y >= thiz->yLim) { // check limitaiton
y = thiz->yLim; // on limit do not integrate, hold the I-part
}
else if (y <= -thiz->yLim) {
y = -thiz->yLim;
}
else if(thiz->disableIntg ==0) { // only if output is not limited, integrate the I-Part.
int32 wxId; // nShKI is 0 in width range, only >0 for Tn >= 5000 * Tctrl
muls16_emC(wxId, wxP >> f->nShKI, f->fI); // growth for integrator in 32 bit width.
thiz->qI += wxId; // integrate
}
}
return thiz->y = y; //use hi part of integrator for output.
}
8. FunctionBlocks in Simulink
Simulink ( ® Mathworks ) is a known system to simulate technical things, and also to build applications by graphical programming (Modelling).
You can have a special Mathworks native infrastructure especially for the code generation via models, but you can also use widely parts in C/++. It is a proper approach to use the same core modules in Simulink as also in other programming environments, immediately in C/++ language or in other modeling tools for graphical programming.
Simulink supports this approach by offering a System of C-language S-Functions. See also
The PID controlling algorithm are preferred to use for that. See an example, the current control of a voltage converter with dq, dqn parts (positive and negative system) after Park-transformation (field oriented) and the ab-controller for DC parts of immediately with the oscillating currents after the Clarke-transformation (3-phase to vector presentation):
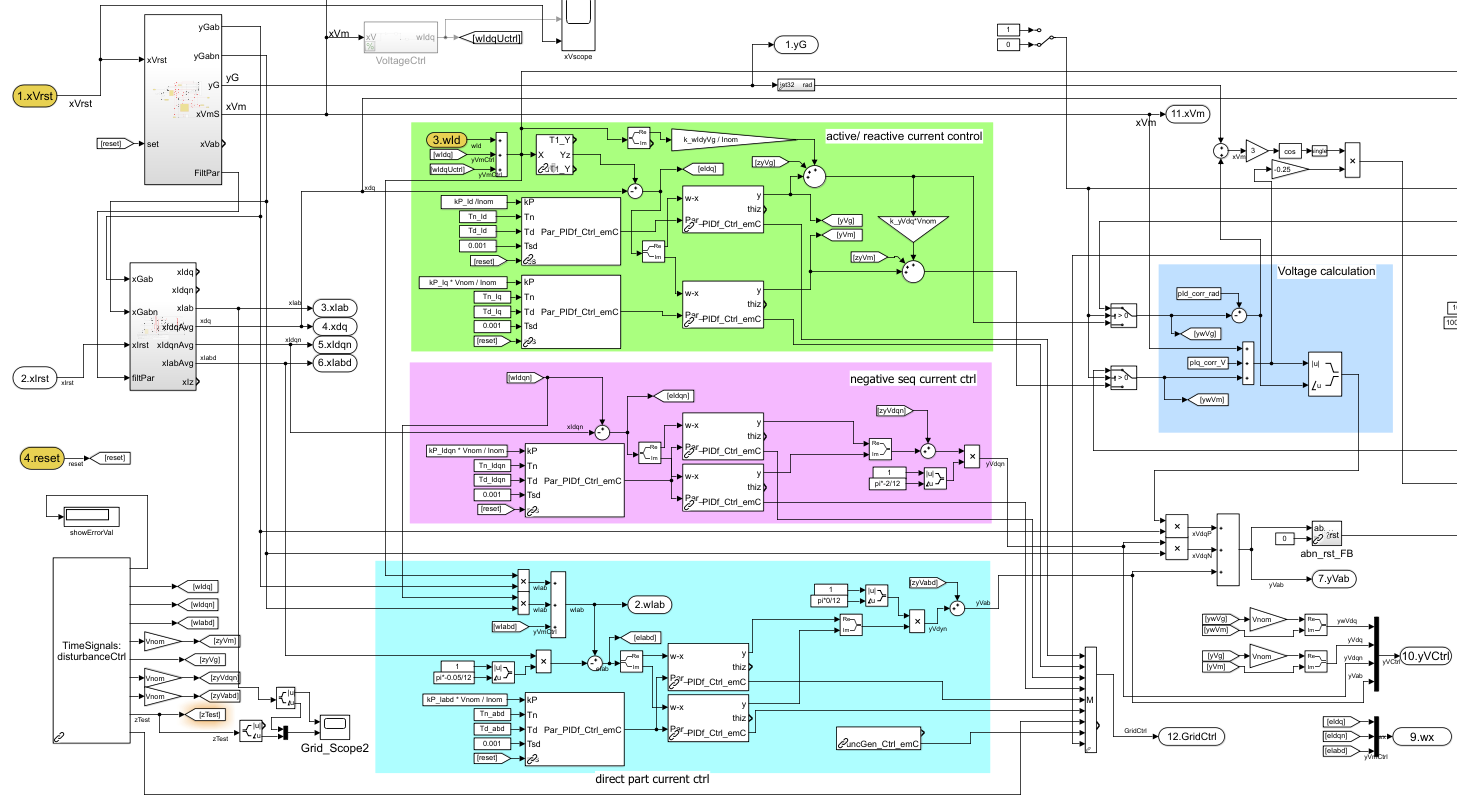
You see 6 controllers, with 4 parameter sets. The parameter are partial constant values but it is possible to substitute the values for more complex contexts.
The shown S-Function blocks (SFBlock) are generated from the header file of the emC/Ctrl/PIFf_Ctrl_emC.h with knowledge of the data struct and operation signature:
The Par_PIDf_Ctrl_emC is a so named 'Object-FB' with own data,
the struct Par_PIDf_Ctrl_emC_s, and the operations for ctor, init and set:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.h /**ctor of Par_PID controller * @param Tstep it is necessary as Simulink parameter to define the association to a defined step time. * It is the time to call the Operation-FB. It is [[set_Par_PIDf_Ctrl_emC(...)]]. * But the argument is not used here. The value is really only necessary for simulink: * * For 4diac, the step time is determined by the event connections. * * For C/++ usage the step time is determined by the calling sequence. * @simulink ctor. */ extern_C Par_PIDf_Ctrl_emC_s* ctor_Par_PIDf_Ctrl_emC ( ObjectJc* othiz, float Tstep); /**init of parameter FBlock for the PID controller. * This operation calls set_Par_PIDf_Ctrl_emC(...) with the given parameter. * The initialization is unconditionally done * @param Tctrl_param The Tstep time of the controller, which should be regard on calculation of the factors. * @param yMax_param Value for scaling of the integer integrator. The maximal value for control must not be greater. * see limit_PIDf_ctrl_emC(...) * @param kP init value for P-gain. It is changable, see set_Par_PIDf_Ctrl_emC(...) * @param Tn init value for Integration time. * It is the time where in step response the same value is reached as given from P-part. * It is changable, see set_Par_PIDf_Ctrl_emC(...) * @param Td init value for Differential time. * It is the time of growth of a ramp where the same value is produced as from P-part. * It is changable, see set_Par_PIDf_Ctrl_emC(...) * @param dt time related to the dx input, describes which period is used for tx. * Note: Use Tctrl for immediately or smoothed dx, use n*Tctrl for delayed dx. * @param reset true then the controller is initial resetted. reset state can be changed with reset_PIDf_Ctrl_emC(...) * @param openLoop_parem true then the PID controller values are calculated but the output is hold, intially on 0. * This is especially and only for manually evaluation of the controlling. * The openLoop state can only be changed for each controller by debug access. * * @simulink init */ extern_C bool init_Par_PIDf_Ctrl_emC ( Par_PIDf_Ctrl_emC_s* thiz, float Tctrl_param, float yMax_param , float kP, float Tn, float Td, float dt, bool reset, bool openLoop_param ); /**step of parameter FBlock for the PID controller for actual changed parameter * @param kP P-gain. It is changable * @param Tn Integration time. * It is the time where in step response the same value is reached as given from P-part. * @param Td init value for Differential time. * It is the time of growth of a ramp where the same value is produced as from P-part. * @param dt time related to the dx input, describes which period is used for tx. * Note: Use Tctrl for immediately or smoothed dx, use n*Tctrl for delayed dx. * @param reset true then the controller is initial resetted. reset state can be changed with reset_PIDf_Ctrl_emC(...) * * @simulink Object-FB, no-thizStep. */ extern_C void set_Par_PIDf_Ctrl_emC ( Par_PIDf_Ctrl_emC_s* thiz , float kP, float Tn, float Td, float dt, bool reset);
There FBlock is immediately a S-Function FBlock with the following Dialog:
As you see, the name of the S-Function itself follows the name of the Object-FB
in the header file. The parameters are that of the ctor_ and init_ with _param on end,
The Mask defines the parameter names and presentation of the mask, excerpt of mask dialog:
With that definition the mask is presented in an application as:
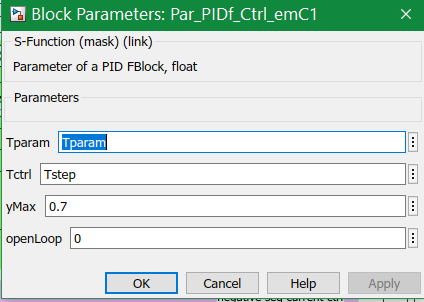
The parameter of the mask are non-tunable parameter, for the ctor and init.
Tunable parameter are possible as values of the 'Object-FB', not used here.
The arguments of the step_Par_PIDf_Ctrl_emC(…) are input values here.
The adequate is for the PIDf_Ctrl_emC SFBLock. (Todo show all?)
The both other FBlocks are so named 'Operation-FB' without own data, as 'methods' or operations of the Object-FB SFBlock:
=>source: src_emC/emC/Ctrl/PIDi_Ctrl_emC.h /**set Limitation of PID controller * @simulink Operation-FB. */ extern_C void setIntg_PIDf_Ctrl_emC(PIDf_Ctrl_emC_s* thiz, float intg, bool set, bool hold, float* intg_y); /**set Limitation of PID controller * @simulink Operation-FB. */ extern_C void setLim_PIDf_Ctrl_emC(PIDf_Ctrl_emC_s* thiz, float lim);